为了探索代数式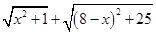 的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作
的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作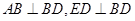 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则
,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则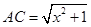 ,
,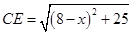 则问题即转化成求AC+CE的最小值.
则问题即转化成求AC+CE的最小值.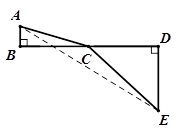
(1)我们知道当A、C、E在同一直线上时, AC+CE的值最小,于是可求得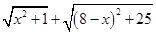 的最小值等于 ,此时
的最小值等于 ,此时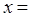 ;
;
(2)请你根据上述的方法和结论,试构图求出代数式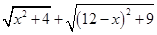 的最小值.
的最小值.
中秋节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.
九(1)班数学建模兴趣小组根据调查,整理出第x天(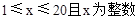 )的捕捞与销售的相关信息如下:
)的捕捞与销售的相关信息如下:
| 鲜鱼销售单价(元/kg) |
20 |
| 单位捕捞成本(元/kg) |
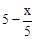 |
| 捕捞量(kg) |
950-10x |
(1)在此期间该养殖场每天的捕捞量与前一天的捕捞量相比是如何变化的?
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(元)之间的函数关系式;(当天收入=日销售额 日捕捞成本)
日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.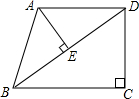
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
已知一次函数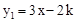 的图象与反比例函数
的图象与反比例函数 的图象相交,其中一个交点的纵坐标为6.
的图象相交,其中一个交点的纵坐标为6.
(1)求两个函数的解析式;
(2)若已知另一点的横坐标为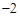 ,结合图象求出
,结合图象求出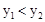 时x的取值范围.
时x的取值范围.
已知二次函数的图像经过点(0,-4),且当x=2,有最大值—2。求该二次函数的关系式:
某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.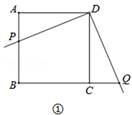
(1)求证:DP=DQ;
(2)如图2,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;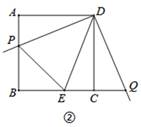
(3)如图3,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.