某市水果批发部门欲将A市的一批水果运往本市销售，有火车和汽车两种运输方式，运输过程中的损耗均为200元/时。其它主要参考数据如下：
| 运输工具 |
途中平均速度 （千米/时） |
运费 （元/千米） |
装卸费用 （元） |
| 火车 |
100 |
15 |
2000 |
| 汽车 |
80 |
20 |
900 |
（1）车的总支出费用比火车费用多1100元，你知道本市与A市之间的路程是多少千米吗？请你列方程解答。
（2）市与某市之间的距离为S千米，且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是A市水果批发部门的经理，要想将这种水果运往其他地区销售。你将选择哪种运输方式比较合算呢？
已知点P的坐标为(－2m，m－6)，根据下列条件分别确定字母m的值或取值范围．
(1)点P在y轴上；
(2)点P在一、三象限的角平分线上；
(3)点P在第三象限．
某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
（1）当每间商铺的年租金定为13万元时,能租出多少间？
（2）当每间商铺的年租金定为多少万元时,该公司的年收益（收益＝租金－各种费用）为275万元？
某农场去年种植了10亩地的南瓜，亩产量为2000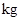
，根据市场需要，今年该农场扩大了种植面积，并且全部种植了高产的新品种南瓜，已知南瓜种植面积的增长率是亩产量的增长率的2倍，今年南瓜的总产量为60 000kg，求南瓜亩产量的增长率．
已知关于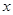
的一元二次方程
（
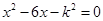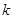为常数）．
（1）求证：方程有两个不相等的实数根；
（2）设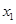
，
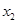为方程的两个实数根，且
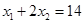，试求出方程的两个实数根和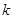的值．
在等腰△ABC中，三边分别为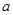
、
、
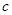，其中
，若关于
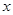的方程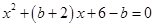
有两个相等的实数根，求△ABC的周长．