在一个可以改变体积的容器内有一定质量的二氧化碳气体，当改变容-优题课

题文

在一个可以改变体积的容器内有一定质量的二氧化碳气体，当改变容器的体积时，气体的密度也会随之改变，密度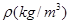与体积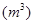之间的函数关系如图所示。

（1）通过图象你能得到什么信息（至少写一条）？
（2）写出与之间函数关系式；
（3）求当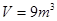时，二氧化碳的密度。

科目数学题型解答题难度中等

知识点：平行线分线段成比例

登录免费查看答案和解析

相关试题

如图，AC=DC，BC=EC，∠ACD=∠BCE．求证：∠A=∠D．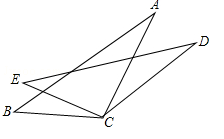

（1）计算：；
（2）化简：．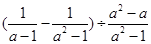

$M$ 如图，已知抛物线 $y = a x^{2} + b x + c$ 经过 $A （ ﹣ 2 ， 0 ）， B （ 4 ， 0 ）， C （ 0 ， 3 ）$ 三点．

（1）求该抛物线的解析式；
（2）在y轴上是否存在点M，使 $△ A C M$ 为等腰三角形？若存在，请直接写出所有满足要求的点M的坐标；若不存在，请说明理由；
（3）若点 $P （ t ， 0 ）$ 为线段 $A B$ 上一动点（不与A，B重合），过 $P$ 作 $y$ 轴的平行线，记该直线右侧与 $△ A B C$ 围成的图形面积为 $S$ ，试确定 $S$ 与 $t$ 的函数关系式．

如图，AB为⊙O的直径，直线CD切⊙O于点D，AM⊥CD于点M，BN⊥CD于N．

（1）求证：∠ADC=∠ABD；
（2）求证：AD²=AM•AB；
（3）若AM=，sin∠ABD=，求线段BN的长．

如图，一次函数与反比例函数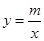的图象交于A（1，4），B（4，n）两点．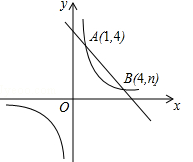

（1）求反比例函数的解析式；
（2）求一次函数的解析式；
（3）点P是x轴上的一动点，试确定点P并求出它的坐标，使PA+PB最小．

试卷网试题网古诗词网作文网范文网