某班同学寒假期间在三个小区进行了一次有关“年夜饭在哪吃”的调查,若年夜饭在家吃的称为“传统族”,否则称为“前卫族”,这两类家庭总数占各自小区家庭总数的比例如下:
| A小区 |
传统族 |
前卫族 |
| 比例 |
 |
 |
| B小区 |
传统族 |
前卫族 |
| 比例 |
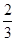 |
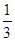 |
| C小区 |
传统族 |
前卫族 |
| 比例 |
 |
 |
(Ⅰ)从A , B , C三个小区中各选一个家庭,求恰好有2个家庭是“传统族”的概率(用比例作为相应的概率);
(Ⅱ)在C小区按上述比例选出的20户家庭中,任意抽取3户家庭,其中“前卫族”家庭的数量记为X,求X的分布列和期望 .
.