(本小题满分12分)某商场销售某种商品的经验表明，该商品每日的销售量
（单位：千克）与销售价格
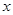（单位：元/千克）满足关系式
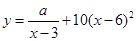，其中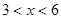
，
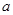为常数，已知销售价格为5元/千克时，每日可售出该商品11千克。
（1）求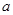的值；
（2）若该商品的成本为3元/千克，试确定销售价格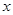的值，使商场每日销售该商品所获得的利润最大。
已知
，
，
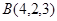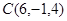，求证其为直角三角形．
如图，已知矩形ABCD中，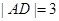
，
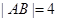．将矩形ABCD沿对角线BD折起，使得面BCD⊥面ABD．现以D为原点，DB作为y轴的正方向，建立如图空间直角坐标系，此时点A恰好在xDy坐标平面内．试求A，C两点的坐标．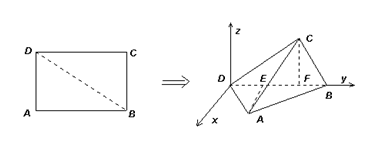 
如图，在四棱锥P－ABCD中，底面ABCD为正方形，且边长为2a，棱PD⊥底面ABCD，PD=2b，取各侧棱的中点E，F，G，H，写出点E，F，G，H的坐标．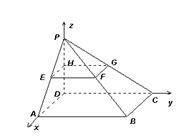
如图，长方体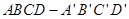
中，
，
，
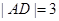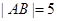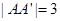，设E为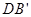
的中点，F为
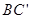的中点，在给定的空间直角坐标系D－xyz下，试写出A，B，C，D，
，
，
，
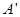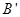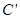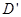，E，F各点的坐标．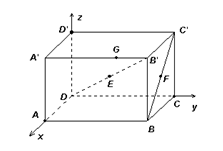
某车间生产一种仪器的固定成本是10000元，每生产一台该仪器需要增加投入100
元，已知总收入满足函数：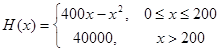
，其中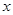
是仪器的月产量.
（1）将利润表示为月产量的函数（用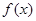
表示）；
（2）当月产量为何值时，车间所获利润最大？最大利润是多少元?（总收入＝总成本＋利润）