在计算“ ”时,先改写第k项:
”时,先改写第k项:  由此得
由此得
 ……
……
相加,得
(1)类比上述方法,请你计算“ ”的结果;
”的结果;
(2) 试用数学归纳法证明你得到的等式.
(本小题满分10分)选修4—5:坐标系与参数方程
在直角坐标系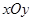 中,半圆C的参数方程为
中,半圆C的参数方程为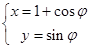 (
(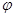 为参数,
为参数,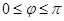 ),以O为极点,x轴的非负半轴为极轴建立极坐标系.
),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求C的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是 ,射线OM:
,射线OM: 与半圆C的交点为O、P,与直线
与半圆C的交点为O、P,与直线 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
(本小题满分12分)已知抛物线y2="2px" (p>0)上点T(3,t)到焦点F的距离为4.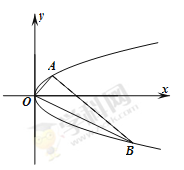
(Ⅰ)求t,p的值;
(Ⅱ)设A、B是抛物线上分别位于x轴两侧的两个动点,且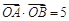 (其中 O为坐标原点).
(其中 O为坐标原点).
(ⅰ)求证:直线AB必过定点,并求出该定点P的坐标;
(ⅱ)过点P作AB的垂线与抛物线交于C、D两点,求四边形ACBD面积的最小值.
(本小题满分12分)如图,PA 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB=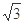 ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.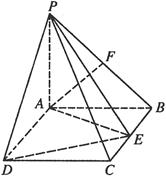
(Ⅰ)当点E为BC的中点时, 证明EF//平面PAC;
(Ⅱ)求三棱锥E-PAD的体积;
(Ⅲ)证明:无论点E在边BC的何处,都有PE AF.
AF.
(本小题满分10分)选修4—5:几何选讲
如图,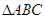 为直角三角形,
为直角三角形,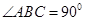 ,以AB为直径的圆交AC于点E,点D是BC边的中点,连接OD交圆O于点M,求证:
,以AB为直径的圆交AC于点E,点D是BC边的中点,连接OD交圆O于点M,求证:
(Ⅰ)O、B、D、E四点共圆;
(Ⅱ)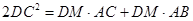 .
.
(本小题满分12分)已知函数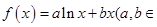 R
R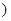 ,曲线
,曲线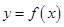 在点
在点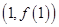 处的切线方程为
处的切线方程为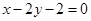 .
.
(Ⅰ)求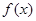 的解析式;
的解析式;
(Ⅱ)当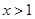 时,
时,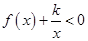 恒成立,求实数
恒成立,求实数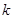 的取值范围;
的取值范围;