已知关于
的一元二次方程
．
（1）求证：当
取不等于l的实数时，此方程总有两个实数根．
（2）若
是此方程的两根，并且
，直线
：
交轴于点A，交
轴于点B，坐标原点O关于直线的对称点O′在反比例函数
的图象上，求反比例函数的解析式．
（3）在（2）的成立的条件下，将直线绕点A逆时针旋转角
，得到直线′，′交轴于点P，过点P作轴的平行线，与上述反比例函数的图象交于点Q，当四边形APQO′的面积为
时，求角
的值．
某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO=8米，母线AB与底面半径OB的夹角为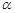
，
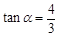，则圆锥的底面积是平方米（结果保留π）．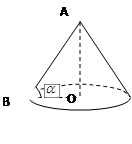
如图，已知△ABC中，AB=AC=10厘米，BC=8厘米，点D为AB的中点．
（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇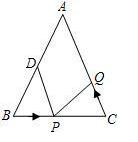
25．如图,△ABC是等腰直角三角形, AB=AC,D是斜边BC的中点，E、F分别是AB、AC边上的点，且DE⊥DF．
（2）请说明：BE² + CF ² = EF ²；
（3）若BE = 6，CF = 8，求△DEF的面积（直接写结果）．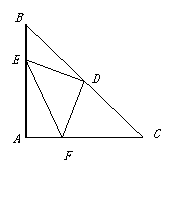
如图，BD是□ABCD的对角线，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．求证：四边形DEBF为平行四边形。
如图，某学校（A点）与公路（直线L）的距离AB为300米，又与公路车站（D点）的距离AD为500米，现要在公路上建一个小商店（C点），使CA=CD，求商店与车站之间的距离CD的长．