一动圆与圆 外切,与圆
外切,与圆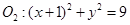 内切.
内切.
(1)求动圆圆心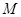 的轨迹
的轨迹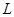 的方程;
的方程;
(2)设过圆心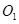 的直线
的直线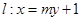 与轨迹
与轨迹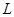 相交于
相交于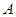 、
、 两点,请问
两点,请问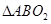 (
(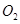 为圆
为圆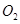 的圆心)的内切圆
的圆心)的内切圆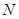 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
(本小题满分13分)
如图,已知四棱锥 的底面是直角梯形,∠ABC
的底面是直角梯形,∠ABC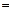 ∠BCD
∠BCD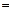 90°,AB
90°,AB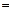 BC
BC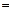 PB
PB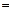 PC
PC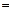 2CD
2CD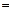 2,侧面PBC⊥底面ABCD。
2,侧面PBC⊥底面ABCD。
(1)求证: ;
;
(2)求二面角 的余弦值。
的余弦值。
(本小题满分13分)
设数列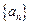 的前
的前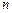 项和为
项和为 ,且满足
,且满足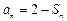
 .
.
(1)求 ,
,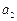 ,
, ,
, 的值并猜想这个数列的通项公式
的值并猜想这个数列的通项公式
(2)证明数列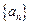 是等比数列.
是等比数列.
(本小题满分12分) 分别是椭圆
分别是椭圆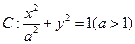 的左右焦点,直线
的左右焦点,直线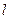 与C相交于A,B两点
与C相交于A,B两点
(1)直线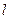 斜率为1且过点
斜率为1且过点 ,若
,若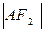 ,
,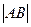 ,
,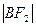 成等差数列,,求
成等差数列,,求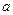 值
值
(2)若直线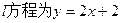 ,且
,且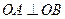 ,求
,求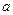 值.
值.
本小题满分12分)
对于任意的实数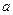 ,不等式
,不等式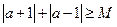 恒成立,记实数
恒成立,记实数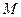 的最大值是
的最大值是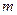 .
.
(1)求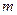 的值;
的值;
(2)解不等式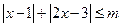 .
.
(本小题满分12分)
已知数列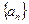 满足
满足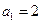 ,且
,且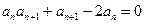 (
(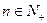 )。
)。
(1)求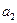 、
、 、
、 的值;
的值;
(2)猜想数列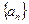 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。