已知椭圆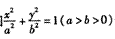 长轴上有一点到两个焦点之间的距离分别为:3+2
长轴上有一点到两个焦点之间的距离分别为:3+2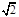 ,3-2
,3-2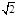
(1)求椭圆的方程;
(2)如果直线x=t(teR)与椭圆相交于A,B,若C(-3,0),D(3,0),证明直线CA与直线
BD的交点K必在一条确定的双曲线上;
(3)过点Q(1,0 )作直线l(与x轴不垂直)与椭圆交于M,N两点,与y轴交于点R,、若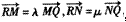 ,求证:
,求证: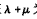 为定值.
为定值.
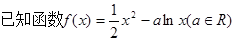 。
。
(1)若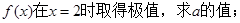
(2)求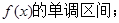
(3)求证:当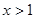 时,
时,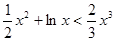 恒成立。
恒成立。
已知公差不为零的等差数列 的前4项和为10,且
的前4项和为10,且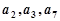 成等比数列.
成等比数列.
(Ⅰ)求通项公式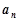 ;
;
(Ⅱ)设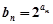 ,求数列
,求数列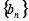 的前
的前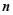 项和
项和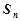 .
.
在平面直角坐标系xOy中,曲线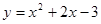 与坐标轴的交点都在圆C上。
与坐标轴的交点都在圆C上。
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C被直线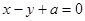 截得的弦长为
截得的弦长为 ,求
,求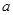 的值。
的值。
某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题: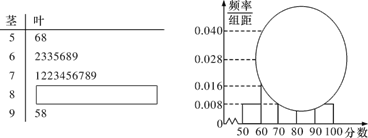
求分数在之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在之间的概率.
如图所示,已知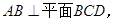 M、N分别是AC、AD的中点,BC
M、N分别是AC、AD的中点,BC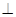 CD.
CD.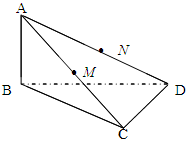
(Ⅰ)求证:MN∥平面BCD;
(Ⅱ)求证:平面B CD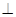 平面ABC;
平面ABC;
(Ⅲ)若AB=1,BC=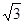 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.