已知函数
(1)求函数 的极值点;
的极值点;
(2)若直线 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线 相切,求直线
相切,求直线 的方程;
的方程;
(3)设函数 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.
上的最小值.
(其中e为自然对数的底数)
某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?最大利润是多少?
若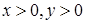 ,且
,且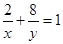 ,求
,求 及
及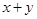 的最小值.
的最小值.
设锐角三角形ABC的内角A、B、C的对边分别为 .
.
(1)求角B的大小;
(2)若a=3 ,c=5,求b.
,c=5,求b.
(1)求不等式的解集: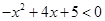 ;
;
(2)求函数的定义域: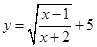 .
.
已知集合A="{x|" 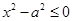 ,其中
,其中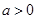 },B="{x|"
},B="{x|" 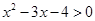 },且A
},且A 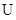 B = R,求实数
B = R,求实数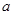 的取值范围.
的取值范围.