如图所示是甲、乙两人追赶过程中路程和时间之间的函数关系图象,由图象回答下列问题:
(1)谁追赶谁?甲、乙两人谁出发早?早几小时?
(2)甲出发几小时后两人相遇?此时他们走了多远?
某校宣传栏中公示了担任下学期七年级班主任的12位老师的情况(见下表),小凤准备到该校就读七年级,请根据表中信息帮小凤进行如下统计分析:
| 姓名 |
性别 |
年龄 |
学历 |
职称 |
姓名 |
性别 |
年龄 |
学历 |
职称 |
|
| 王雄辉 |
男 |
35 |
本科 |
高级 |
蔡波 |
男 |
45 |
大专 |
高级 |
|
| 李红 |
男 |
40 |
本科 |
中级 |
李凤 |
女 |
27 |
本科 |
初级 |
|
| 刘梅英 |
女 |
40 |
中专 |
中级 |
孙焰 |
男 |
40 |
大专 |
中级 |
|
| 张英 |
女 |
43 |
大专 |
高级 |
彭朝阳 |
男 |
30 |
大专 |
初级 |
|
| 刘元 |
男 |
50 |
中专 |
中级 |
龙妍 |
女 |
25 |
本科 |
初级 |
|
| 袁桂 |
男 |
30 |
本科 |
初级 |
杨书 |
男 |
40 |
本科 |
中级 |
(1)该校下学期七年级班主任老师年龄的众数是多少?
(2)在图7(1)中,将反映老师学历情况的条形统计图补充完整;
(3)在图7(2)中,标注扇形统计图中表示老师职称为初级和高级的百分比;
(4)小凤到该校就读七年级,班主任老师是女老师的概率是多少?
|

如图,在梯形ABCD中,AB∥CD,AD =DC,求证:AC是∠DAB的平分线.
计算: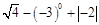 .
.
在平面直角坐标系中,抛物线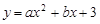 与
与 轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)直接填写: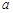 =,b=,顶点C的坐标为;
=,b=,顶点C的坐标为;
(2)在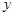 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标. 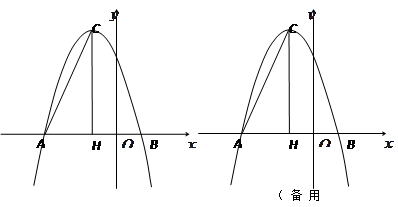
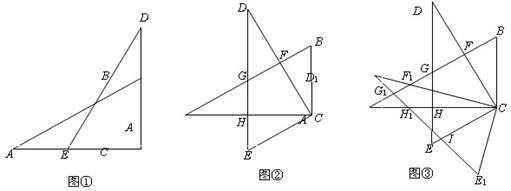
两个大小相同且含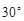 角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转
角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转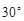 得到图②,点F、G分别是CD、DE与AB的交点,点H是DE与AC的交点.
得到图②,点F、G分别是CD、DE与AB的交点,点H是DE与AC的交点.
(1)不添加辅助线,写出图②中所有与△BCF全等的三角形;
(2)将图②中的△DEC绕点C逆时针旋转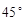 得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
(3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.