已知平行四边形ABCD,从平面ABCD外一点 引向量
引向量 ,
,
(1)求证:四点 共面;
共面;
(2)平面ABCD 平面EFGH.
平面EFGH.
(本小题满分13分)某学校实验室有浓度为 和
和 的两种
的两种 溶液.在使用之前需要重新配制溶液,具体操作方法为取浓度为
溶液.在使用之前需要重新配制溶液,具体操作方法为取浓度为 和
和 的两种
的两种 溶液各
溶液各 分别装入两个容积都为
分别装入两个容积都为 的锥形瓶
的锥形瓶 中,先从瓶
中,先从瓶 中取出
中取出 溶液放入
溶液放入 瓶中,充分混合后,再从
瓶中,充分混合后,再从 瓶中取出
瓶中取出 溶液放入
溶液放入 瓶中,再充分混合.以上两次混合过程完成后算完成一次操作.设在完成第
瓶中,再充分混合.以上两次混合过程完成后算完成一次操作.设在完成第 次操作后,
次操作后, 瓶中溶液浓度为
瓶中溶液浓度为 ,
, 瓶中溶液浓度为
瓶中溶液浓度为 .
.
(1)请计算 ,并判定数列
,并判定数列 是否为等比数列?若是,求出其通项公式;若不是,请说明理由;
是否为等比数列?若是,求出其通项公式;若不是,请说明理由;
(2)若要使得 两个瓶中的溶液浓度之差小于
两个瓶中的溶液浓度之差小于 ,则至少要经过几次?
,则至少要经过几次?
(本小题满分12分)如图,在三棱柱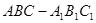 中,
中,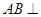 侧面
侧面 ,已知
,已知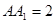 ,
,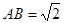 ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)当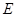 点为棱
点为棱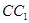 的中点时,求
的中点时,求 与平面
与平面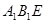 所成的角的正弦值.
所成的角的正弦值.
(本小题满分12分)已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图所示,从这10名学生中随机抽取两名成绩不低于73分的学生, 求被抽取到的两名学生的成绩之和不小于154分的概率.
(本小题满分12分)已知 且
且 .设函数
.设函数
(1)求函数 的解析式;
的解析式;
(2)若在锐角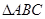 中,
中, ,边
,边 ,求
,求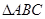 周长的最大值.
周长的最大值.
(本小题满分13分) 已知函数 (
( ).
).
(1)求函数 的单调区间;
的单调区间;
(2)函数 在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
(3)若 ,当
,当 时,不等式
时,不等式 恒成立,求α的取值范围.
恒成立,求α的取值范围.