（本小题满分12分）
若关于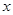
的实系数方程
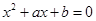有两个根，一个根在区间
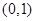内，另一根在区间
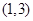内，记点
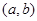对应的区域为
．
（1）设
，求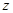
的取值范围；
（2）过点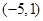
的一束光线，射到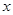轴被反射后经过区域，求反射光线所在直线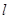
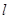经过区域内的整点（即横纵坐标为整数的点）时直线的方程.
设函数
，用单调性定义证明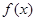
在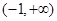
上是减函数.
已知集合
，
.
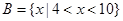（1）求 
，
；
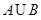（2）求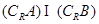
.
化简求值：
，其中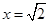
.
（本题14分）已知圆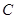
经过
，
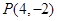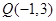两点，且在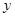
轴上截得的线段长为
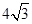，半径小于5．
（1）求直线
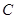与圆的方程；
（2）若直线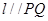
，且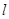
与圆C交于点A，B，且以线段AB为直径的圆经过坐标原点，求直线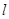的方程．
（本题13分）已知某种植物种子每粒成功发芽的概率都为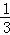
，某植物研究所进行该种子的发芽实验，每次实验种一粒种子，每次实验结果相互独立．假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的．若该研究所共进行四次实验，设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值；
（1）求随机变量ξ的数学期望；
（2）记“关于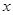
的不等式
的解集是实数集R”为事件A，求事件A发生的概率
．