(本小题满分13分)(注意:在试题卷上作答无效)
已知函数 的反函数为
的反函数为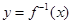 ,定义:若对给定的实数
,定义:若对给定的实数 ,函数
,函数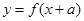 与
与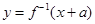 互为反函数,则称
互为反函数,则称 满足“
满足“ 和性质”.
和性质”.
(1)判断函数 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2)若 ,其中
,其中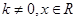 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得 对任意的
对任意的 恒成立?若存在,求出
恒成立?若存在,求出 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
已知椭圆 的对称中心为坐标原点,上焦点为
的对称中心为坐标原点,上焦点为 ,离心率
,离心率 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 为
为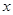 轴上的动点,过点
轴上的动点,过点 作直线
作直线 与直线
与直线 垂直,试探究直线
垂直,试探究直线 与椭圆
与椭圆 的位置关系.
的位置关系.
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数 及天数如下表:
及天数如下表:
售出个数 |
10 |
11 |
12 |
13 |
14 |
15 |
| 天数 |
3 |
3 |
3 |
6 |
9 |
6 |
试依据以频率估计概率的统计思想,解答下列问题:
(Ⅰ)计算小王某天售出该现烤面包超过13个的概率;
(Ⅱ)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量. 试求小王增加订购量的概率.
(Ⅲ)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
已知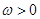 ,函数
,函数 的最小正周期为
的最小正周期为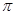 .
.
(Ⅰ)试求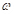 的值;
的值;
(Ⅱ)在图中作出函数 在区间
在区间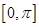 上的图象,并根据图象写出其在区间
上的图象,并根据图象写出其在区间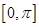 上的单调递减区间.
上的单调递减区间.
已知函数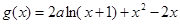
(1)当 时,讨论函数
时,讨论函数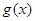 的单调性:
的单调性:
(2)若函数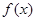 的图像上存在不同两点
的图像上存在不同两点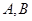 ,设线段
,设线段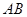 的中点为
的中点为 ,使得
,使得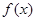 在点
在点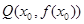 处的切线
处的切线 与直线
与直线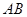 平行或重合,则说函数
平行或重合,则说函数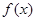 是“中值平衡函数”,切线
是“中值平衡函数”,切线 叫做函数
叫做函数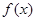 的“中值平衡切线”。试判断函数
的“中值平衡切线”。试判断函数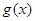 是否是“中值平衡函数”?若是,判断函数
是否是“中值平衡函数”?若是,判断函数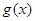 的“中值平衡切线”的条数;若不是,说明理由.
的“中值平衡切线”的条数;若不是,说明理由.
已知椭圆C: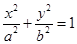 的离心率等于
的离心率等于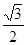 ,点P
,点P 在椭圆上。
在椭圆上。
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左右顶点分别为
的左右顶点分别为 ,过点
,过点 的动直线
的动直线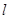 与椭圆
与椭圆 相交于
相交于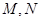 两点,是否存在定直线
两点,是否存在定直线 :
: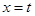 ,使得
,使得 与
与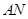 的交点
的交点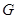 总在直线
总在直线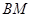 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的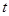 值;若不存在,说明理由.
值;若不存在,说明理由.