小王经营一家面包店，每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元，若当天卖不完，则未卖出的现烤面包因过期每个亏损5元.经统计，得到在某月（30天）中，小王每天售出的现烤面包个数
及天数如下表：
| 售出个数 |
10 |
11 |
12 |
13 |
14 |
15 |
| 天数 |
3 |
3 |
3 |
6 |
9 |
6 |
试依据以频率估计概率的统计思想，解答下列问题：
（Ⅰ）计算小王某天售出该现烤面包超过13个的概率；
（Ⅱ）若在今后的连续5天中，售出该现烤面包超过13个的天数大于3天，则小王决定增加订购量. 试求小王增加订购量的概率.
（Ⅲ）若小王每天订购14个该现烤面包，求其一天出售该现烤面包所获利润的分布列和数学期望.
已知向量
，且
（1）求
的值
（2）求
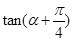的值
函数
.
（1）若
，函数
在区间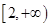
上是单调递增函数，求实数
的取值范围；
（2）设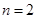
，若对任意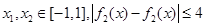
恒成立，求的取值范围．
某小区想利用一矩形空地
建市民健身广场，设计时决定保留空地边上的一水塘（如图中阴影部分），水塘可近似看作一个等腰直角三角形，其中
，
，且
中，
，经测量得到
．为保证安全同时考虑美观，健身广场周围准备加设一个保护栏．设计时经过点
作一直线交
于
，从而得到五边形
的市民健身广场，设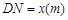
．
（1）将五边形的面积
表示为
的函数；
（2）当
为何值时，市民健身广场的面积最大？并求出最大面积．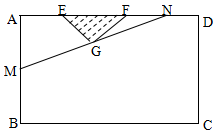
已知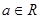
，函数
.
⑴若不等式
对任意
恒成立，求实数
的最值范围；
⑵若
，且函数
的定义域和值域均为
，求实数的值.
在数列
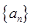中，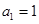
，
．
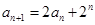（1）设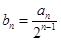
．证明：数列
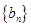是等差数列；
（2）求数列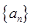的前
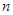项和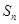
．