我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直接坐标系如图①所示,如果把锅纵断面的抛物线的记为C1,把锅盖纵断面的抛物线记为C2.
(1)求C1和C2的解析式;
(2)如图②,过点B作直线BE:y= x﹣1交C1于点E(﹣2,﹣
x﹣1交C1于点E(﹣2,﹣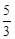 ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
(3)如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.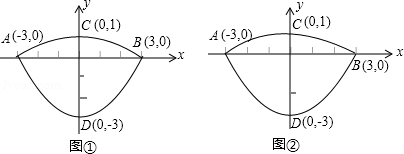
一次函数y= x的图像如图所示,它与二次函数y=ax2-4ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
x的图像如图所示,它与二次函数y=ax2-4ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D.
①若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的关系式;
②若CD=AC,且△ACD的面积等于10,求此二次函数的关系式.
已知二次函数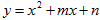 的图像经过点
的图像经过点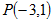 ,对称轴是经过
,对称轴是经过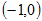 且平行于
且平行于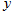 轴的直线。
轴的直线。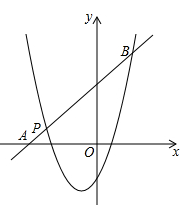
(1)求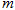 、
、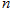 的值
的值
(2)如图,一次函数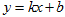 的图像经过点
的图像经过点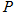 ,与
,与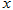 轴相交于点
轴相交于点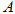 ,与二次函数的图像相交于另一点B,点B在点P的右侧,
,与二次函数的图像相交于另一点B,点B在点P的右侧,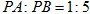 , 求一次函数的表达式。
, 求一次函数的表达式。
已知如图,在平面直角坐标系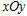 中,直线
中,直线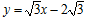 与
与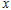 轴、
轴、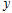 轴分别交于A,B两点,P是直线AB上一动点,⊙
轴分别交于A,B两点,P是直线AB上一动点,⊙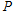 的半径为1.
的半径为1.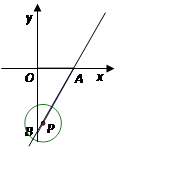
(1)判断原点O与⊙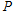 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当⊙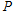 过点B时,求⊙
过点B时,求⊙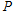 被
被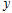 轴所截得的劣弧的长;
轴所截得的劣弧的长;
(3)当⊙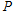 与
与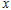 轴相切时,求出切点的坐标.
轴相切时,求出切点的坐标.
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.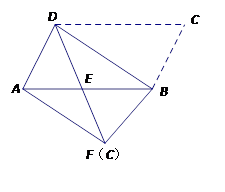
(1)求证: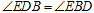 ;
;
(2)判断AF与BD是否平行,并说明理由.
如图,把△EFP按图所示的方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上.已知EP=FP= ,EF=
,EF= ,∠BAD=60°,且AB
,∠BAD=60°,且AB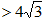 .
.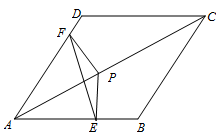
(1)求∠EPF的大小;
(2)若AP=6,求AE+AF的值;
(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.