(本小题满分12分)
某园林局对1000株树木的生长情况进行调查,其中杉树 600株,槐树400株 .现用分层抽样方法从这1000株树木中随机抽取100株,杉树与槐树的树干周长(单位:cm)的抽查结果如下表:
| 树干周长 (单位:cm ) |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
| 杉 树 |
6 |
19 |
21 |
 |
| 槐 树 |
4 |
20 |
 |
6 |
(I)求 ,
, 值及估计槐树树干周长的众数;
值及估计槐树树干周长的众数;
(Ⅱ)如果杉树的树干周长超过60cm就可以砍伐,请估计该片园林可以砍伐的杉树有多少株?
(Ⅲ)树干周长在30cm到40cm之间的4株槐树有1株患虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.
已知函数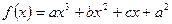 (
(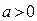 )的单调递减区间是
)的单调递减区间是 ,且满足
,且满足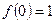 .
.
(Ⅰ)求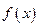 的解析式;
的解析式;
(Ⅱ)对任意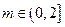 , 关于
, 关于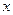 的不等式
的不等式 在
在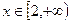 上有解,求实数
上有解,求实数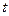 的取值范围.
的取值范围.
某化工厂生产的某种化工产品,当年产量在150吨至250吨之内,其年生产的总成本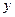 (万元)与年产量
(万元)与年产量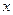 (吨)之间的关系可近似地表示为
(吨)之间的关系可近似地表示为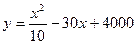
(1)当年产量为多少吨时,每吨的平均成本最低,并求每吨最低平均成本
(2)若每吨平均出厂价为16万元,求年生产多少吨时,可获得最大的年利润,并求最大年利润。
设函数 ,其中向量
,其中向量 ,
,
(1)求函数 的最小正周期和单调递增区间
的最小正周期和单调递增区间
(2)当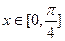 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
已知数列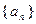 、
、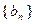 满足
满足 ,
,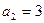 ,
,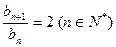 ,
, 。
。
(1)求数列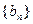 的通项公式;
的通项公式;
(2)数列 满足
满足
 ,求
,求 。
。
已知过点P(1,9)的直线m与x轴和y轴的正半轴分别交于A,B两点,O为坐标原点,求:
(1)当 取最小值时的直线m的方程;
取最小值时的直线m的方程;
(2)当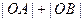 取最小值时的直线m的方程。
取最小值时的直线m的方程。