(1)如图1，在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=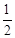
∠ABC(0°＜∠CBE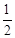＜∠ABC)。以点B为旋转中心，将△BEC按逆时针方向旋转∠ABC，得到△BE’A（点C与点A重合，点E到点E’处），连接DE’。求证：DE’="DE."
（2）如图2，在△ABC中，BA=BC，∠ABC=90°，D，E是AC边上的两点，
且满足∠DBE=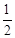∠ABC(0°＜∠CBE＜45°).求证：DE2=AD2+EC2.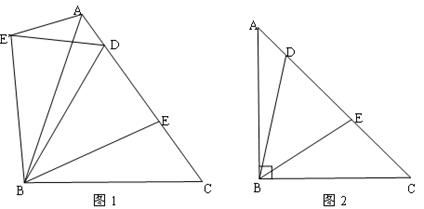
（·湖州市 第19题 6分）已知y是x的一次函数，当x=3时，y=1；当x=−2时，y=−4，求这个一次函数的解析式．
（·杭州市 第23题 12分）方成同学看到一则材料，甲开汽车，乙骑自行车从M地出发沿一条公路匀速前往N地，设乙行驶的时间为t（h），甲乙两人之间的距离为y（km），y与t的函数关系如图1所示，方成思考后发现了图1的部分正确信息，乙先出发1h，甲出发0．5小时与乙相遇，……，请你帮助方成同学解决以下问题：
（1）分别求出线段BC，CD所在直线的函数表达式
（2）当20＜y＜30时，求t的取值范围
（3）分别求出甲、乙行驶的路程S甲、S乙与时间t的函数表达式，并在图2所给的直角坐标系中分别画出它们的图象
（4）丙骑摩托车与乙同时出发，从N地沿同一条公路匀速前往M地，若丙经过
h与乙相遇，问丙出发后多少时间与甲相遇？
（·杭州市 第20题 10分）设函数y=（x−1）[（k−1）x+（k−3）]（k是常数）
（1）当k取1和2时的函数y1和y2的图象如图所示，请你在同一直角坐标系中画出当k取0时函数的图象
（2）根据图象，写出你发现的一条结论
（3）将函数y2的图象向左平移4个单位，再向下平移2个单位，得到函数y3的图象，求函数y3的最小值:
（·衢州市 第19题 6分）如图，已知点A（a，3）是一次函数y1=x+b图象与反比例函数y2=
图象的一个交点．
（1）求一次函数的解析式；
（2）在y轴的右侧，当y1＞y2时，直接写出x的取值范围．
（·温州卷 第19题 8分）某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核。甲、乙、丙各项得分如下表：
| 笔试 |
面试 |
体能 |
|
| 甲 |
83 |
79 |
90 |
| 乙 |
85 |
80 |
75 |
| 丙 |
80 |
90 |
73 |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序；
（2）该公司规定：笔试、面试、体能分分别不得低于80分、80分、70分，并按60%，30%，10%的比例计入总分。根据规定，请你说明谁将被录用。