(·温州卷 第19题 8分)某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核。甲、乙、丙各项得分如下表:
| |
笔试 |
面试 |
体能 |
| 甲 |
83 |
79 |
90 |
| 乙 |
85 |
80 |
75 |
| 丙 |
80 |
90 |
73 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该公司规定:笔试、面试、体能分分别不得低于80分、80分、70分,并按60%,30%,10%的比例计入总分。根据规定,请你说明谁将被录用。
已知:如图,直线 与反比例函数图象
与反比例函数图象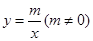 分别交于点
分别交于点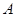 和点
和点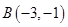 两点,与
两点,与 轴交于点
轴交于点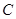 ,且以
,且以 为顶点的三角形面积为
为顶点的三角形面积为 ,点
,点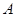 横坐标为
横坐标为 .
.
(1)则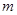 =;
=;
(2)当 =1时,求
=1时,求 的值;
的值;
(3)求 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围.
的取值范围.
如图,点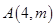 是反比例函数
是反比例函数 (x>0)的图象上一点,
(x>0)的图象上一点,
 轴正半轴于
轴正半轴于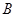 ,
, 是
是 的中点;一次函数
的中点;一次函数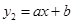 的图象过
的图象过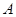 、
、 两点,并交于
两点,并交于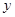 轴于
轴于 .
.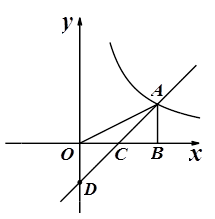
(1)直接写出点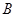 、
、 的坐标;
的坐标;
(2)求一次函数和反比例函数的解析式;
(3)观察图象,请指出在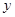 轴的右侧,当
轴的右侧,当 时
时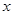 的取值范围.
的取值范围.
甲、乙两辆汽车同时分别从 、
、 两城沿同一条高速公路匀速驶向
两城沿同一条高速公路匀速驶向 城.已知
城.已知 、
、 两城的距离为
两城的距离为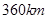 ,
, 、
、 两城的距离为
两城的距离为 ,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为
,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为 km/h.
km/h.
(1)根据题意填写下表:
| 行驶的路程(km) |
速度(km/h) |
所需时间(h) |
|
| 甲车 |
360 |
||
| 乙车 |
320 |
 |
(2)求甲、乙两车的速度.
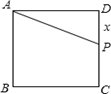
如图,正方形 的边长为
的边长为 ,
,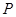 是
是 边上一点.设
边上一点.设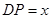 ,四边形
,四边形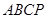 的面积为
的面积为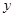 .
.
(1)求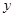 关于
关于 的函数关系式,并写出自变量x的取值范围;
的函数关系式,并写出自变量x的取值范围;
(2)画出(1)中的这个函数图象.
已知 是
是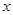 的一次函数,且当
的一次函数,且当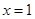 时,
时, ;当
;当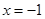 时,
时,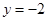 .
.
(1)求这个函数的解析式;
(2)求出这条直线与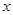 轴的交点坐标.
轴的交点坐标.