如图，在平面直角坐标系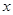
O
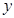中，矩形AOCD的顶点A的坐标是（0,4），现有两动点P、Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度，匀速向点C运动，点Q从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动.点P，Q同时出发，同时停止，设运动时间为t秒，当t=2秒时PQ=
.
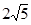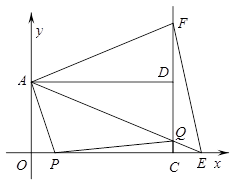
（1）求点D的坐标，并直接写出t的取值范围；
（2）连接AQ并延长交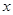轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF，则△AEF的面积S是否随t的变化而变化？若变化，求出S与t的函数关系式；若不变化，求出S的值.
（3）在（2）的条件下，t为何值时，四边形APQF是梯形？
如图，已知“中国渔政310”船（A）在南海执行护渔任务，接到陆地指挥中心（P）命令，得知出事渔船（B）位于陆地指挥中心西南方向，位于“中国渔政310”船正南方向，“中国渔政310”船位于陆地指挥中心北偏西60°方向，距离为80海里的地方．而“中国渔政310”船最大航速为20海里/时．根据以上信息，请你求出“中国渔政310”船接到命令后赶往渔船出事地点最少需要多少时间（结果保留根号）？
如图，我区某中学计划用一块空地修建一个学生自行车车棚，其中一面靠墙，这堵墙的长度为12米.计划建造车棚的面积为80平方米，已知现有的板材可使新建的板墙的总长为24米.为方便学生出行，学校决定在与墙平行的一面开一个2米宽的门.求这个车棚的长和宽分别是多少米？
先化简，再求值：
，其中
.
如图，在平面直角坐标系xOy中，AB在x轴上，AB=10，以AB为直径的⊙
与y轴正半轴交于点C，连接BC、AC，CD是⊙的切线，AD⊥CD于点D，tan∠CAD=
，抛物线
过A、B、C三点.
（1）求证：∠CAD=∠CAB；
（2）求抛物线的解析式；
（3）判断抛物线的顶点E是否在直线CD上，并说明理由.
某商店经销甲、乙两种商品. 现有如下信息:
请根据以上信息，解答下列问题：
（1）甲、乙两种商品的进货单价各多少元?
（2）该商店平均每天卖出甲商品600件和乙商品400件．经调查发现，甲、乙两种商品零售单价分别每降0.1元，这两种商品每天可各多销售100件．为了使每天获取更大的利润，商店决定把甲、乙两种商品的零售单价都下降m元. 在不考虑其他因素的条件下，当m定为多少时，才能使商店每天销售甲、乙两种商品获取的利润最大？每天的最大利润是多少?