一辆值勤的警车停在公路边,当警员发现从他旁边以10 m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5 s后警车发动起来,并以2.5 m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90 km/h以内.问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
如图所示,两根平行的光滑金属导轨MN、PQ放在水平面上,左端向上弯曲,导轨间距为L,电阻不计。水平段导轨所处空间存在方向竖直向上的匀强磁场,磁感应强度为B。导体棒a与b的质量均为m,电阻值分别为Ra=R,Rb=2R。b棒放置在水平导轨上足够远处,a棒在弧形导轨上距水平面h高度处由静止释放。运动过程中导体棒与导轨接触良好且始终与导轨垂直,重力加速度为g。
(1)求a棒刚进入磁场时受到的安培力的大小和方向;
(2)求最终稳定时两棒的速度大小;
(3)从a棒开始下落到最终稳定的过程中,求b棒上产生的内能。
宇航员驾驶宇宙飞船到达月球,他在月球表面做了一个实验:在离月球表面高度为h处,将一小球以初速度v0水平抛出,水平射程为x。已知月球的半径为R,万有引力常量为G。不考虑月球自转的影响。求:
(1)月球表面的重力加速度大小g0 ;
(2)月球的质量M;
(3)飞船在近月圆轨道绕月球做匀速圆周运动的速度v。
如图所示,斜面AC长L= 1m,倾角θ =37°,CD段为与斜面平滑连接的水平地面。一个质量m = 2kg的小物块从斜面顶端A由静止开始滑下。小物块与斜面、地面间的动摩擦因数均为μ = 0.5。不计空气阻力,g = 10m/s2,sin37°= 0.6,cos37°= 0.8。求:
(1)小物块在斜面上运动时的加速度大小a;
(2)小物块滑到斜面底端C点时的速度大小v;
(3)小物块在水平地面上滑行的最远距离x。
如图所示,宽度为L的粗糙平行金属导轨PQ和P′Q′倾斜放置,顶端QQ′之间连接一个阻值为R的电阻和开关S,底端PP′处与一小段水平轨道用光滑圆弧相连。已知底端PP′离地面的高度为h,倾斜导轨处于垂直于导轨平面的匀强磁场(图中未画出)中。若断开开关S,一根质量为m、电阻为r、长也为L的金属棒从AA′处由静止开始滑下,金属棒落地点离PP′的水平距离为x1;若闭合开关S,该金属棒仍从AA′处由静止开始滑下,则金属棒落地点离PP′的水平距离为x2。不计导轨电阻,忽略金属棒经过PP′处的机械能损失,已知重力加速度为g,求: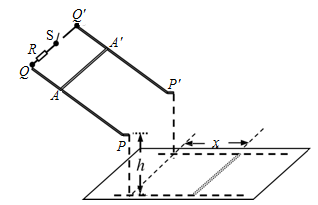
(1)开关断开时,金属棒离开底端PP′的速度大小;
(2)开关闭合时,在下滑过程金属棒中产生的焦耳热。
(3)开关S仍闭合,金属棒从比AA′更高处由静止开始滑下,水平射程仍为x2,请定性说明金属棒在倾斜轨道上运动的规律。
质量m=2.0×10-4kg、电荷量q=﹢1.0×10-6C的带电微粒静止在空间范围足够大的匀强电场中,电场强度大小为E1。在t=0时刻,电场强度的大小突然增加到E2=4.0×103N/C,电场方向保持不变;到t1=0.20s时刻再把电场方向改为水平向右,场强大小E2保持不变。取g=10m/s2。求:
(1)电场强度E1的大小;
(2)t1=0.20s时刻带电微粒的速度大小;
(3)带电微粒在速度方向为水平向右时刻的动能。