如图,在平面直角坐标系中,函数 的图象
的图象 是第一、三象限的角平分线.
是第一、三象限的角平分线.
实验与探究:由图观察易知A(0,2)关于直线 的对称点
的对称点 的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线
的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线 的对称点
的对称点 、
、 的位置,并写出它们的坐标:
的位置,并写出它们的坐标:  、
、 ;
;
归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线 的对称点
的对称点 的坐标为 ;
的坐标为 ;
运用与拓广:已知两点D(0,-3)、E(-1,-4),试在直线 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
若P为△ABC所在平面上一点,且∠APB=∠BP C=∠CPA=120°,则点P叫做△ABC的费马点.
(1)若点P为锐角△ABC的费马点,且∠ABC=60°,PA=3,PC=4,则PB的值为________;
(2)如图,在锐角△ABC外侧作等边△ACB′连结BB′.
求证:BB′过△ABC的费马点P,且BB′=PA+PB+PC.
先阅读理解下面的例题,再按要求解答:
例题:解一元二次不等式x·x-9﹥0
解:∵x·x-9=(x+3)(x-3)
∴(x+3)(x-3)﹥0.
由有理数的乘法法则“两数相乘,同号得正”,有
(1) (2)
(2)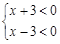
解不等式组(1),得x﹥3,
解不等式组(2),得x﹤-3,
故(x+3)(x-3)﹥0的解集为x﹥3或x﹤-3,
即一元二次不等式 的解集为x﹥3或x﹤-3.
的解集为x﹥3或x﹤-3.
问题:求分式不等式﹤0的解集.
在平面直角坐标系中,一动点P( ,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动。图②是P点运动的路程s(个单位)与运动时间
,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动。图②是P点运动的路程s(个单位)与运动时间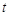 (秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(1)求s与
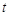 之间的函数关系式。
之间的函数关系式。(2)求与图③相对应的P点的运动路径;及P点出发多少秒首次到达点B;
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图③中补全函数图象.
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+(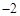 )=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移
)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移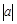 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移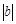 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
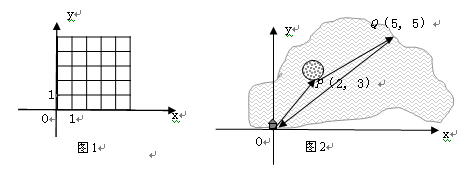
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 .
.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形. (3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线
实验与探究: 
(1)由图观察易知A(0,2)关于直线l的对称点
 的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5) 关于直线l的对称点
的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5) 关于直线l的对称点 、
、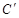 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:  、
、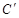 ;
;
归纳与发现:(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点
 的坐标为
的坐标为
运用与拓广:(3)已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.