一个口袋中有4个相同的小球，分别与写有字母A，B，C，D，随机地抽出一个小球后放回，再随机地抽出一个小球．
（1）使用列表法或画树状图法中的一种，列举出两次抽出的球上字母的所有可能结果；
（2）求两次抽出的球上字母相同的概率．
已知：如图，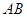
// 
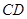，求图形中的x的值.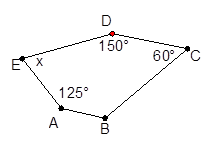
如图，EF∥AD，∠1=∠2, 将求证AB∥DG的过程填空完整.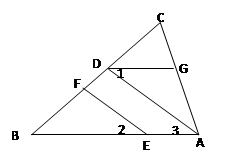
证明：∵EF∥AD（）
∴∠2=（）
又∵∠1=∠2（）
∴∠1=∠3（）
∴AB∥（）
如图为了确定各建筑物的位置：（1）以火车站为原点建立直角坐标系．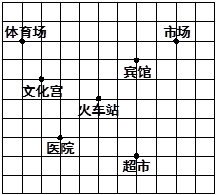
（2）写出市场、超市的坐标.
、
（3）请将体育场、宾馆和火车站看作三点用线段连起来，得△ABC，然后将此三角形向下平移4 个单位长度,再画出平移后的△A/B/C/.
（4）△ABC的面积是_________
如图，已知直角梯形ABCD中，AD∥BC，AB⊥BC ，AD＝2cm，AB＝8cm，CD＝10cm．
(1)求梯形ABCD的周长；
(2)动点P从点B出发，以1cm/s的速度沿B→A→D→C方向向点C运动；动点Q从点C出发，以1cm/s的速度沿C→D→A方向向点A运动；过点Q作QF⊥BC于点F．若P、Q两点同时出发，当其中一点到达终点时整个运动随之结束，设运动时间为t秒．问：
在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．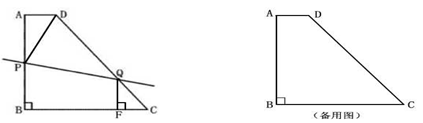
如图，将边长为3cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD的中点 M处，点C落在点N处，MN与CD交于点P， 连接EP．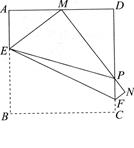
(1) △AEM的周长=_____cm；（2）求证：EP=AE+DP；