如图,某小区准备在一直角围墙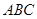 内的空地上植造“绿地
内的空地上植造“绿地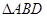 ”,其中
”,其中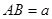 ,
,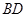 长可根据需要进行调节(
长可根据需要进行调节(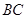 足够长),现规划在
足够长),现规划在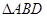 内接正方形
内接正方形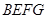 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积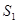 与种花的面积
与种花的面积 的比
的比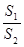 为
为 ,
,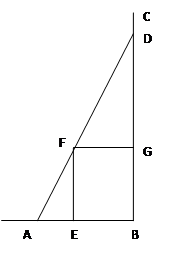
(1)设角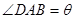 ,将
,将 表示成
表示成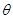 的函数关系;
的函数关系;
(2)当 为多长时,
为多长时, 有最小值,最小值是多少?
有最小值,最小值是多少?
正四棱锥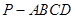 中,
中,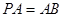 ,点M,N分别在PA,BD上,且
,点M,N分别在PA,BD上,且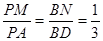 .
.
(Ⅰ)求异面直线MN与AD所成角;
(Ⅱ)求证: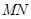 ∥平面PBC;
∥平面PBC;
(Ⅲ)求MN与平面PAB所成角的正弦值.
已知圆C的半径为2,圆心在x轴的正半轴上,直线 与圆C相切.
与圆C相切.
(I)求圆C的方程;
(II)过点Q(0,-3)的直线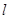 与圆C交于不同的两点A
与圆C交于不同的两点A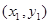 、B
、B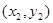 ,当
,当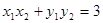 时,求△AOB的面积.
时,求△AOB的面积.
已知向量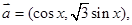
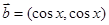 ,函数
,函数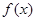

(Ⅰ)求函数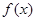 在
在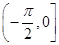 上的值域;
上的值域;
(Ⅱ)当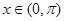 时,若
时,若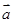 与
与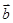 共线,求
共线,求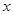 的值.
的值.
已知数列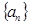 中,
中, ,n≥2时
,n≥2时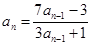 ,求通项公式.
,求通项公式.