某工厂计划生产A、B两种产品共50件，需购买甲、乙两种材料．生产一件A产品需甲种材料30千克、乙种材料10千克；生产一件B产品需甲、乙两种材料各20千克．经测算，购买甲、乙两种材料各1千克共需资金40元，购买甲种材料2千克和乙种材料3千克共需资金105元．
（1）甲、乙两种材料每千克分别是多少元？
（2）现工厂用于购买甲、乙两种材料的资金不超过38000元，且生产B产品不少于28件，问符合条件的生产方案有哪几种？
（3）在（2）的条件下，若生产一件A产品需加工费200元，生产一件B产品需加工费300元，应选择哪种生产方案，使生产这50件产品的成本最低？（成本=材料费+加工费）
关于x的方程x﹣2m=﹣3x+4与2﹣m=x的解互为相反数．
（1）求m的值；
（2）求这两个方程的解．
先化简，再求值：
x2﹣（2x2+2xy﹣
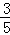y2）+（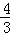
x2﹣xy﹣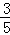y2），其中x=﹣3，y=2．
解方程
（1）4﹣3（2﹣x）=5x
（2）
．
若有理数x，y满足（x+1）2=16，|2y﹣1|=9，且|x+y|=﹣x﹣y，求3x+2y﹣xy的值．
甲骑摩托车，乙骑自行车从相距25km的两地相向而行．
（1）甲、乙同时出发经过0.5小时相遇，且甲每小时行驶路程是乙每小时行驶路程的3倍少6km，求乙骑自行车的速度．
（2）在甲骑摩托车和乙骑自行车与（1）相同的前提下，若乙先出发0.5小时，甲才出发，问：甲出发几小时后两人相遇？