如图，在Rt△ABC中，∠ACB=90°，AC=6㎝，BC=8㎝，P为BC的中点．动点Q从点P出发，沿射线PC方向以2㎝/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．
⑴当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；
⑵已知⊙O为△ABC的外接圆，若⊙P与⊙O相切，求t的值．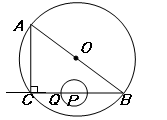
如图所示，在平面直角坐标系中，M是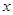
轴正半轴上一点，⊙M与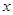轴的正半轴交于A、B两点，A在B的左侧，且OA、OB的长是方程
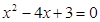的两根，ON是⊙M的切线，N为切点，N在第四象限．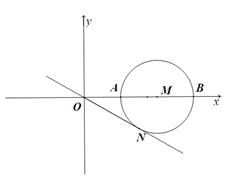
（1）求⊙M的直径；
（2）求直线ON的函数关系式；
（3）在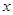轴上是否存在一点T，使△OTN是等腰三角形？若存在，求出T的坐标；若不存在，请说明理由．
如图，有一面积为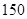
米2的长方形鸡场，鸡场的一边靠墙（墙长
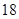米），另三边用竹篱笆围成，如果竹篱笆的长为
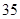米，求鸡场的长与宽各为多少米？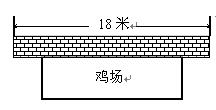
如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC，过点D作DE⊥AC，垂足为E．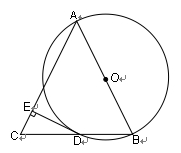
（1）求证：AB=AC；(2)求证DE为⊙O的切线．
如图，一个圆锥的高为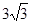
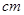,侧面展开图是半圆，求：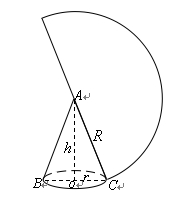
（1）圆锥的底面半径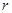
与母线
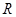之比；
（2）圆锥的全面积．
已知关于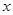
的一元二次方程
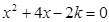有两个实数根，求
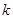的取值范围及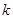的负整数值．