已知箱子中有10个球,期中8个是正品,2个是次品,若每次取出1个球,取出后不放回,求:
(1)取两次就能取到2个正品的概率;
(2)取三次才能取到2个正品的概率;
(3)取四次才能取到2个正品的概率.
如图,已知过点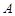
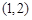 的抛物线
的抛物线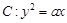 与过点
与过点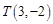 的动直线
的动直线 相交于
相交于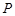 、
、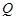 两点.
两点.
(Ⅰ)求直线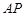 与直线
与直线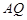 的斜率的乘积;
的斜率的乘积;
(Ⅱ)若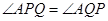 ,求证:△
,求证:△ 的周长为定值.
的周长为定值.
如图,在四棱锥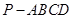 中,平面PAD⊥平面ABCD,
中,平面PAD⊥平面ABCD,  ,
,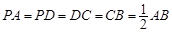 ,E是BD的中点.
,E是BD的中点.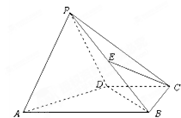
(Ⅰ)求证:EC//平面APD;
(Ⅱ)求BP与平面ABCD所成角的正切值;
(Ⅲ)求二面角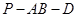 的正弦值.
的正弦值.
已知等差数列数列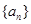 的前
的前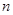 项和为
项和为 ,等比数列
,等比数列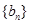 的各项均为正数,公比是
的各项均为正数,公比是 ,且满足:
,且满足: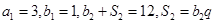 .
.
(Ⅰ)求 与
与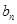 ;
;
(Ⅱ)设 ,若
,若 满足:
满足: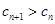 对任意的
对任意的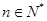 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 中,三个内角A、B、C所对的边分别为
中,三个内角A、B、C所对的边分别为 、
、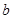 、
、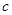 ,若
,若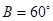 ,
,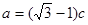 .
.
(Ⅰ)求角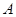 的大小;
的大小;
(Ⅱ)已知 的面积为
的面积为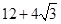 ,求函数
,求函数 的最大值.
的最大值.
已知函数 ,设方程
,设方程 有两个实数根
有两个实数根
(1)若果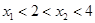 ,设函数
,设函数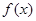 的对称轴为
的对称轴为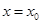 ,求证:
,求证: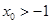
(2)如果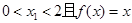 的两个实数根相差2,求实数b的取值范围。
的两个实数根相差2,求实数b的取值范围。