已知函数f(x)=sinωx·sin(
-φ)-sin(+ωx)sin(π+φ)是R上的偶函数.其中ω>0,0≤φ≤π,其图象关于点M(
,0)对称,且在区间[0,]上是单调函数,求φ和ω的值.
设函数f(x)=msinx+cosx(x∈R)的图象经过点(
,1).
(1)求f(x)的解析式,并求函数的最小正周期.
(2)若f(α+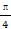
)=
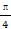且α∈(0,),求f(2α-)的值.
设函数f(x)=2cos2x+2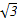
sinxcosx-1(x∈R).
(1)化简函数f(x)的表达式,并求函数f(x)的最小正周期.
(2)若x∈[0,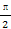
],求函数f(x)的最大值与最小值.
已知函数f(x)=cos2(x-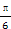
)-sin2x.
(1)求f(
)的值.
(2)若对于任意的x∈[0,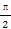
],都有f(x)≤c,求实数c的取值范围.
函数f(x)=
sin2x-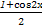
-
.
(1)若x∈[
,
],求函数f(x)的最值及对应的x的值.
(2)若不等式[f(x)-m]2<1在x∈[,]上恒成立,求实数m的取值范围.
的前
项和为
，等比数列
的各项均为正数，公比是
，且满足：
．
与
；
，若
满足：
对任意的
恒成立，求
的取值范围．