已知椭圆
：
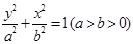的右顶点为
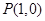，过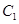的焦点且垂直长轴的弦长为
．
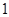（I）求椭圆的方程；
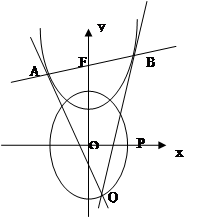
（II）设抛物线
：
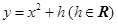的焦点为F，过F点的直线
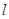交抛物线与A、B两点，过A、B两点分别作抛物线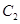的切线交于Q点，且Q点在椭圆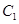上，求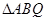
面积的最值，并求出取得最值时的抛物线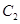的方程。
设
的三内角
所对的边长分别为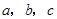
，且
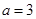，A=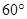
，
．
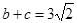（1）求三角形ABC的面积；
（2）求
的值及中内角B,C的大小.
已知函数
(
,
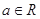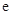为自然对数的底数).
(1)若曲线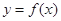
在点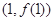
处的切线平行于
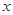轴,求
的值;
(2)求函数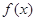
的极值;
(3)当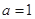
的值时,若直线
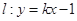与曲线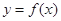没有公共点,求
的最大值.
已知圆C:
,直线L：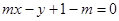
.
（1）求证：对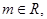
直线L与圆C总有两个不同交点；
（2）设L与圆C交于不同两点A、B，求弦AB的中点M的轨迹方程；
（3）若定点P（1,1）分弦AB所得向量满足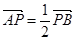
，求此时直线L的方程.
在数列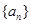
中，已知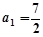
，
（
.
（1）求证：
是等差数列；
（2）求数列
的通项公式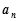
及它的前
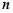项和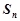
.
如图,直三棱柱ABC-A1B1C1中，D、E分别是AB、BB1的中点.
(1)证明:BC1//平面A1CD；
(2)设AA1=AC=CB=2,AB=
，求三棱锥C一A1DE的体积.