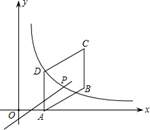
如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE= ,A(3,0),D(-1,0),E(0,3).
,A(3,0),D(-1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量 (件)与销售单价
(件)与销售单价 (元)的关系可以近似的看作一次函数(如图).
(元)的关系可以近似的看作一次函数(如图).
(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)设公司获得的总利润(总利润 总销售额
总销售额 总成本)为
总成本)为 元,求
元,求 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;根据题意判断:当
的取值范围;根据题意判断:当 取何值时,
取何值时, 的值最大?最大值是多少?
的值最大?最大值是多少?
(3)若公司要保证利润不能低于4000元,则销售单价x的取值范围为多少元(可借助二次函数的图像解答)? 
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3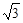 ,AE=3,求AF的长.
,AE=3,求AF的长.
某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.
(1)求该同学看中的随身听和书包单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),该同学只带了400元钱,他能否在这两家超市都可以买下看中的这两样商品?若两家都可以选择,在哪一家购买更省钱?
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y= (x>0)的函数图象经过点D,点P是一次函数
(x>0)的函数图象经过点D,点P是一次函数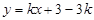
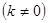 的图象与该反比例函数图象的一个公共点.
的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数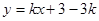
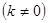 的图象一定过点C;
的图象一定过点C;
(3)对于一次函数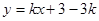
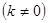 ,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).
,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).