已知一次函数y=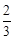 x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数 (x>0)的图象相交于C点.
(x>0)的图象相交于C点.
(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数 (x>0)的关系式.
(x>0)的关系式.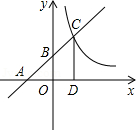
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.
(1)求证:DE与⊙O相切;
(2)连结AD,己知BC=10,BE=2,求sin∠BAD的值.
如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.
(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(结果精确到0.1m).
(参考数据:tan31°≈ ,sin31°≈
,sin31°≈ ,tan39°≈
,tan39°≈ ,sin39°≈
,sin39°≈ )
)
如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
如图,在平面直角坐标系中, 的三个顶点坐标分别为
的三个顶点坐标分别为 (
( ,1),
,1), (
( ,4),
,4), (
( ,2).
,2).
(1)画出 关于
关于 轴对称的图形
轴对称的图形 ,并直接写出
,并直接写出 点坐标;
点坐标;
(2)以原点 为位似中心,位似比为1:2,在
为位似中心,位似比为1:2,在 轴的左侧,画出
轴的左侧,画出 放大后的图形
放大后的图形 ,并直接写出
,并直接写出 点坐标;
点坐标;
(3)如果点 (
( ,
, )在线段
)在线段 上,请直接写出经过(2)的变化后
上,请直接写出经过(2)的变化后 的对应点
的对应点 的坐标.
的坐标.
如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连接AC,BC,作∠APC的平分线交AC于点D.
下列结论正确的是(写出所有正确结论的序号)
①△CPD∽△DPA;
②若∠A=30°,则PC= BC;
BC;
③若∠CPA=30°,则PB=OB;
④无论点P在AB延长线上的位置如何变化,∠CDP为定值.