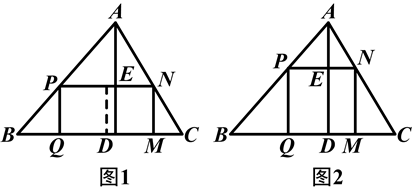
在如图所示的2005年1月份日历中，
| 星期日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
| |
|
|
|
|
|
1 |
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 16 |
17 |
18 |
19 |
20 |
21 |
22 |
| 23 |
24 |
25 |
26 |
27 |
28 |
29 |
| 30 |
31 |
|
|
|
|
|
（1）用一个长方形的方框圈出任意3×3个数，如果从左下角到右上角的“对角线”上的3个数字的和为39，那么这9个数的和为 ；
（2）这个长方形的方框圈出的9个数的和能为216吗？答 ：（填“能”或“不能”）；
（3）如果任意选择如上的阴影部分，那么其中的四个数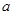
、
、
、
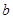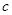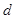又有什么规律呢？请用含的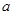、、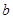、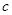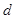等式表示： 。
（其中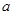、、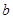、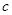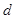四个数之间的大小关系是
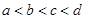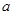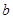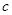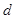，、、、整数）
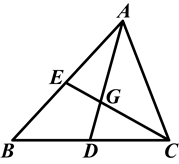
如图，△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G．求证：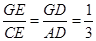
．
如图，在6×8网格图中，每个小正方形边长均为1，点O和△ABC的顶点均为小正方形的顶点．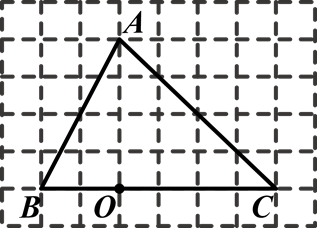
（1）以O为位似中心，在网格图中作△A′B′C′，使△A′B′C′和△ABC位似，且位似比为1︰2；
（2）连接（1）中的AA′，求四边形AA′C′C的周长．（结果保留根号）
在网格图中，画出相应的图形．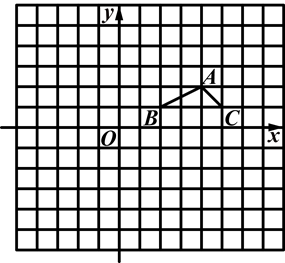
（1）将图形沿x轴负方向平移3个单位，得到△A1B1C1；
（2）关于x轴对称，得到△A2B2C2；
（3）以点C2为位似中心，各边扩大到原来的2倍，得到△A3B3C3．
（陕西）某一天，小明和小亮来到一河边，想用遮阳帽和皮尺测量这条河的大致宽度，两人在确保无安全隐患的情况下，先在河岸边选择了一点B（点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸）．
①小明在B点面向树的方向站好，调整帽檐，使视线通过帽檐正好落在树的底部点D处，如图所示，这时小亮测得小明眼睛距地面的距离AB＝1.7米；
②小明站在原地转动180°后蹲下，并保持原来的观察姿态（除身体重心下移外，其他姿态均不变），这时视线通过帽檐落在了DB延长线上的点E处，此时小亮测得BE＝9.6米，小明的眼睛距地面的距离CB＝1.2米．
根据以上测量过程及测量数据，请你求出河宽BD是多少米．
（浙江绍兴）课本中有一道作业题：
小颖解得此题的答案为48mm．小颖善于反思，她又提出了如下的问题．
（1）如果原题中所要加工的零件是一个矩形，且此矩形是由两个并排放置的正方形所组成的，如图，此时，这个矩形零件的两条边长又分别为多少mm？请你计算；
（2）如果原题中所要加工的零件只是一个矩形，如图，这样，此矩形零件的两条边长就不能确定，但这个矩形面积有最大值，求达到这个最大值时矩形零件的两条边长．