如图所示,在双缝干涉实验中,S1和S2为双缝,P是光屏上的一点,已知P点与S1、S2距离之差为2.1 ×10-6 m,分别用A、B两种单色光在空气中做双缝干涉实验,问P点是亮条纹还是暗条纹?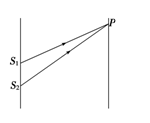
(1)已知A光在折射率为n=1.5的介质中波长为4×10-7 m.
(2)已知B光在某种介质中波长为3.15×10-7 m,当B光从这种介质射向空气时,临界角为37°.
(3)若用A光照射时,把其中一条缝遮住,试分析光屏上能观察到的现象.
如图所示,内径均匀的直角细玻璃管ABC两端开口,AB段竖直,BC段水平,AB=100cm,BC=40cm,在水平段BC内有一长10cm的水银柱,其左端距B点10cm,环境温度为330 K时,保持BC段水平,将玻璃管A端缓慢竖直向下插入大水银槽中,使A端在水银面下10cm。已知大气压为75cmHg且保持不变,若环境温度缓慢升高,求温度升高到多少K时,水银柱刚好全部溢出。
如图甲所示,一个n=10匝,面积为S=0.3m2的圆形金属线圈,其总电阻为R1="2Ω," 与R2=4Ω的电阻连接成闭合电路。线圈内存在方向垂直于纸面向里,磁感应强度按B1="2t" + 3 (T)规律变化的磁场。电阻R2两端通过金属导线分别与电容器C的两极相连.电容器C紧靠着带小孔a(只能容一个粒子通过)的固定绝缘弹性圆筒。圆筒内壁光滑,筒内有垂直水平面竖直向下的匀强磁场B2,O是圆筒的圆心,圆筒的内半径为r=0.4m.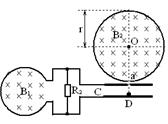
(1)金属线圈的感应电动势E和电容器C两板间的电压U;
(2)在电容器C内紧靠极板且正对a孔的D处有一个带正电的粒子从静止开始经电容器C加速后从a孔垂直磁场B2并正对着圆心O进入筒中,该带电粒子与圆筒壁碰撞四次后恰好又从小孔a射出圆筒.已知粒子的比荷q/m=5×107(C/kg),该带电粒子每次与筒壁发生碰撞时电量和能量都不损失,不计粒子重力和空气阻力,则磁感应强度B2多大(结果允许含有三角函数式)。
潜艇部队经常开展鱼雷攻击敌方舰艇演练。某次演习的简化模型为:敌舰沿直线MN匀速航行,潜艇隐蔽在Q点不动,Q到MN的距离QO="2000" m。当敌舰到达距离O点800 m的A点时,潜艇沿QO方向发射一枚鱼雷,正好在O点击中敌舰。敌舰因受鱼雷攻击,速度突然减为原来的一半,且立刻沿原运动方向做匀加速运动逃逸。100s后潜艇沿QB方向发射第二枚鱼雷,鱼雷在B点再次击中敌舰。测得OB="1500" m,不考虑海水速度的影响,潜艇和敌舰可视为质点,鱼雷的速度大小恒为25 m/s。求: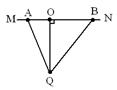
(1)敌舰第一次被击中前的速度;
(2)鱼雷由Q至B经历的时间;
(3)敌舰逃逸时的加速度大小。
图中左侧部分为过山车简易模型装置,它是由弧形轨道PQ、竖直圆轨道MQ和水平轨道QN组成。所有轨道都光滑且之间均平滑对接,圆形轨道半径R=0.5m,一质量为m1=1kg的小球a从离水平轨道高为h=5m的地方沿弧形轨道静止滑下,经圆轨道运动一周后与静止在N处的小物块b发生正碰,碰后小球a沿原路返回到M点时,对轨道的压力恰好为0。碰后小物块b滑上一足够长的木板c上,已知物块b与木板c之间的动摩擦因数为μ1=0.4,木板c与地面之间的动摩擦因数μ2=0.1,物块b的质量为m2=3kg,木板c的质量为m3=4.5kg,g取10m/s2,求:
(1)小球a第一次经过圆形轨道最低点时的速度;
(2)碰后瞬间小物块b的速度;
(3)木板c运动的总位移。
如图所示,在xoy平面的第四象限内存在沿y轴正方向的匀强磁场,场强大小为E,第一象限存在一有界匀强磁场,方向垂直于xoy平面向里,磁感应强度为B,磁场上边界与x轴正向夹角θ=30°,直线MN与y轴平行,N点坐标为(L,0),现从MN上的P点无初速度释放质量为m,电荷量为q的带正电粒子,不计粒子的重力,求: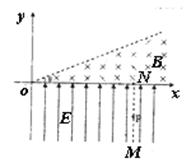
(1)若粒子进入磁场后将垂直于上边界射出磁场,求PN之间的距离;
(2)若粒子进入磁场后能再次回到电场中,则PN之间的距离应满足什么条件?