如图, 中,
中, ,
, 为
为 的中点.
的中点.
操作:过点 做
做 的垂线,过点
的垂线,过点 作
作 的平行线,两直线相交于点
的平行线,两直线相交于点 ,在
,在 的延长线上截取
的延长线上截取 ,联结
,联结 、
、 .
.


(1)试判断 与
与 之间有怎样的关系,并证明你所得的结论;
之间有怎样的关系,并证明你所得的结论;
(2)如果 ,
, ,求
,求 的长.
的长.
如图, 是格点(横、纵坐标都为整数的点)三角形,请在图中画出与
是格点(横、纵坐标都为整数的点)三角形,请在图中画出与 全等的一个格点三角形.
全等的一个格点三角形.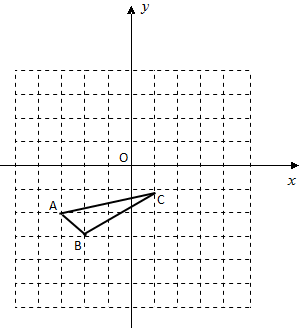
如图, 在平面直角坐标系中,
在平面直角坐标系中, 若
若 、
、 的长是关于
的长是关于 的一元二次方程
的一元二次方程 的两个根,且
的两个根,且
(1)求 的值.
的值.
(2)若 为
为 轴上的点,且
轴上的点,且 求经过
求经过 、
、 两点的直线的解析式,并判断
两点的直线的解析式,并判断 与
与 是否相似?
是否相似?
(3)若点 在平面直角坐标系内,则在直线
在平面直角坐标系内,则在直线 上是否存在点
上是否存在点 使以
使以 、
、 、
、 、
、 为顶点的四边形为菱形?若存在,请直接写出
为顶点的四边形为菱形?若存在,请直接写出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
某冰箱厂为响应国家“家电下乡”号召,计划生产 、
、 两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
| 型号 |
A型 |
B型 |
| 成本(元/台) |
2200 |
2600 |
| 售价(元/台) |
2800 |
3000 |
(1)冰箱厂有哪几种生产方案?
(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
(3)若按(2)中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.
已知 中,
中, 为
为 边的中点,
边的中点,
 绕
绕 点旋转,它的两边分别交
点旋转,它的两边分别交 、
、 (或它们的延长线)于
(或它们的延长线)于 、
、
当 绕
绕 点旋转到
点旋转到 于
于 时(如图1),易证
时(如图1),易证
当 绕
绕 点旋转到
点旋转到 不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立, 、
、 、
、 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
甲、乙两车同时从 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向 地行驶.甲车先到达
地行驶.甲车先到达 地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离
地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离 (千米)与乙车行驶时间
(千米)与乙车行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)请将图中的()内填上正确的值,并直接写出甲车从 到
到 的行驶速度;
的行驶速度;
(2)求从甲车返回到与乙车相遇过程中 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围.
的取值范围.
(3)求出甲车返回时行驶速度及 、
、 两地的距离.
两地的距离.