已知圆
，圆
，动点
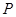到圆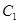
,
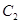上点的距离的最小值相等.
（1）求点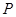的轨迹方程；
（2）点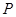的轨迹上是否存在点
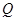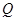，使得点到点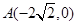
的距离减去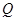点到点
的距离的差为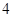
，如果存在求出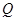点坐标，如果不存在说明理由.
（本小题满分13分）
某出版公司为一本畅销书定价如下: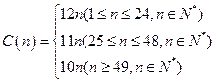
.这里n表示定购书
的数量,C（n）是定购n本书所付的钱数（单位:元）
（1）有多少个n,会出现买多于n本书比恰好买n本书所花钱少?
（2）若一本书的成本价是5元,现有两人来买书,每人至少买1本,两人共买60本,问出版公司至少能赚多少钱?最多能赚多少钱?
(本题满分12分) 已知函数
的图象与函数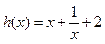
的图象关于点A
（0，1）对称.（1）求函数的解析式（2）若
=+
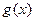，且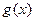在区间（0，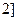
上的值不小于
，求实数
的取值范围.
（本小题满分12分）函数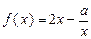
的定义域为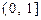
（
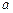为实数）.
（1）当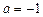
时，求函数
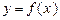的值域；
（2）若函数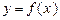在定义域上是减函数，求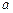的取值范围；
（3）函数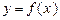在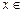
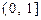上的最大值及最小值，并求出函数取最值时
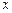的值.
(本题满分12分) 已知
的反函数为
，
.
(1)若
，求
的取值范围D；
(2)设函数
，当
时，求函数
的值域.
（本小题满分12分）已知函数
在定义域
上为增函数，且满足
(1)求
的值 (2)解不等式