（本小题满分13分）
已知
的展开式中第五项的系数与第三项的系数的比是10:1
（1）求展开式中各项系数的和；
（2）求展开式中含
的项；
已知函数
（1）是否存在实数
，使函数
是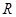
上的奇函数，若存在求出
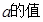，若不存在，也要说明理由．
（2）探索函数的单调性，并利用定义加以证明．
（3）
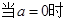求函数的值域．
提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度
（单位：千米/小时）是车流密度
（单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明；当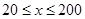
时，车流速度是车流密度的一次函数．
（1）当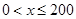
时，求函数
的表达式．
（2）当车流密度为多大时，车流量（单位时间内通过桥上某观查点的车辆数，单位：
辆/每小时）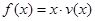
可以达到最大，并求最大值（精确到1辆/每小时）．
已知函数
．（
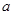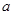>0且≠1．）
（1）求f（x）的定义域．
（2）判断f（x）的奇偶性并予以证明．
（3）当0<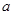<1时，求使f（x）＞0的x的解集．
设函数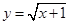
的定义域为集合
，不等式
的解集为集合
．
（1）求集合，；（2）求集合
，
．
不用计算器计算：
．