在△ABC中,AB、BC、AC三边的长分别为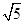 、
、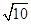 、
、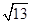 ,求这个三角形的面积.
,求这个三角形的面积.
小华同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样就不需要求△ABC的高,而借用网格就能计算出它的面积.(本题8分)
⑴ 请你将△ABC的面积直接填写在横线上.
思维拓展:
⑵ 我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为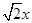 、
、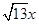 、
、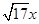 (
(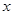 >0),请利用图②的正方形网格(每个小正方形的边长为
>0),请利用图②的正方形网格(每个小正方形的边长为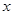 )画出相应的△ABC,并求出它的面积.
)画出相应的△ABC,并求出它的面积.
探索创新:
⑶ 若△ABC三边的长分别为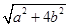 、
、 、
、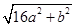 (
(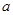 >0,
>0,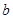 >0,且
>0,且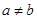 ),试运用构图法求出这个三角形的面积.
),试运用构图法求出这个三角形的面积.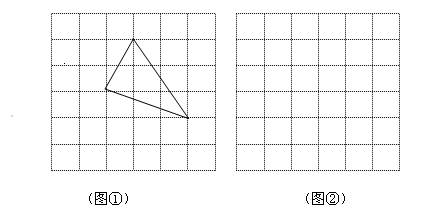
已知抛物线抛物线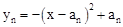 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为(,);
依此类推第n条抛物线yn的顶点坐标为(,);
所有抛物线的顶点坐标满足的函数关系是;
(3)探究下列结论:
①若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
②是否存在经过点A(2,0)的直线和所有抛物线都相交,且被每一条抛物线截得得线段的长度都相等?若存在,直接写出直线的表达式;若不存在,请说明理由.
如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示,量得连杆OA长为10cm,雨刮杆AB长为48cm,∠OAB=1200.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.
(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)
(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)
(参考数据:sin60°= ,cos60°=
,cos60°= ,tan60°=
,tan60°= ,
,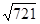 ≈26.851,可使用科学计算器)
≈26.851,可使用科学计算器)
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.
(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.
生活中很多矿泉水没有喝完便被扔掉,造成极大的浪费,为此数学兴趣小组的同学对某单位的某次会议所用矿泉水的浪费情况进行调查,为期半天的会议中,每人发一瓶500ml的矿泉水,会后对所发矿泉水喝的情况进行统计,大至可分为四种:A:全部喝完;B:喝剩约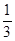 ;C:喝剩约一半;D:开瓶但基本未喝.同学们根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:
;C:喝剩约一半;D:开瓶但基本未喝.同学们根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题: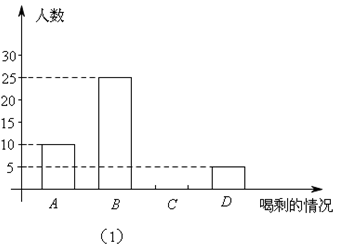
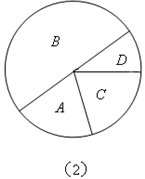
(1)参加这次会议的有多少人?在图(2)中D所在扇形的圆心角是多少度?并补全条形统计图;(计算结果请保留整数).
(2)若开瓶但基本未喝算全部浪费,试计算这次会议平均每人浪费的矿泉水约多少毫升?
(3)据不完全统计,该单位每年约有此类会议60次,每次会议人数约在40至60人之间,请用(2)中计算的结果,估计该单位一年中因此类会议浪费的矿泉水(500ml/瓶)约有多少瓶?(可使用科学计算器)
如图,在平面直角坐标系中,反比例函数 (x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6) .
(x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6) .
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.