(本小题满分12分)某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185)得到的频率分布直方图如图所示。
(Ⅰ)求第3、4、5组的频率;
(Ⅱ)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求:第4组至少有一名学生被甲考官面试的概率?
(本小题满分12分)已知数列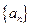 满足
满足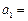
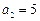 ,
,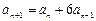 (
(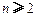 ,
,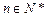 ),
),
若数列 是等比数列.(1)求数列
是等比数列.(1)求数列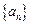 的通项公式;(2)求证:当
的通项公式;(2)求证:当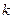 为奇数时,
为奇数时,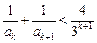 ;(3)求证:
;(3)求证: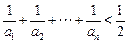 (
(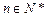 ).
).
已知函数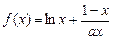 ,其中为大于零的常数.(1)若函数
,其中为大于零的常数.(1)若函数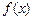 在
在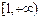 上单调递增,求
上单调递增,求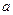 的取值范围;(2)求函数
的取值范围;(2)求函数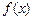 在区间
在区间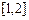 上的最小值;(3)求证:对于任意的
上的最小值;(3)求证:对于任意的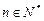 且
且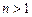 时,都有
时,都有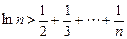 成立.
成立.
已知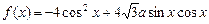 ,将
,将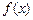 的图象向左平移
的图象向左平移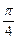 个单位后所得的图象关于
个单位后所得的图象关于 对称.(1)求实数
对称.(1)求实数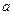 ,并求出
,并求出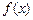 取得最大值时的集合;(2)求
取得最大值时的集合;(2)求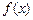 的最小正周期,并求
的最小正周期,并求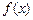 在
在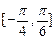 上的值域.
上的值域.
已知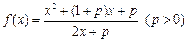
(1)若p > 1时,解关于x的不等式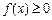 ;
;
(2)若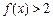 对
对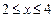 时恒成立,求p的范围.
时恒成立,求p的范围.
数列{an}中a1 = 2,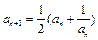 ,{bn}中
,{bn}中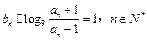 .
.
(1)求证:数列{bn}为等比数列,并求出其通项公式;
(2)当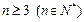 时,证明:
时,证明: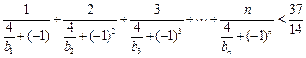 .
.