如图,在三棱柱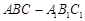 中,已知
中,已知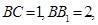
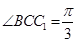
 侧面
侧面
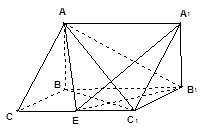
(Ⅰ)求直线C1B与底面ABC所成角正切值;
(Ⅱ)在棱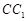 (不包含端点
(不包含端点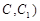 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(Ⅲ)在(2)的条件下,若 ,求二面角
,求二面角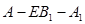 的大小.
的大小.
(本小题满分10分)选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系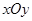 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为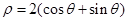 ,斜率为
,斜率为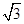 的直线
的直线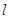 交y轴于点
交y轴于点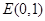 .
.
(1)求C的直角坐标方程,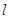 的参数方程;
的参数方程;
(2)直线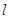 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求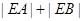 .
.
(本小题满分10分)选修4-1:几何证明选讲
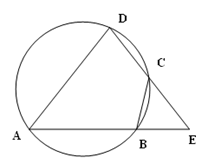
如图,四边形 是
是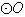 的内接四边形,
的内接四边形,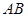 的延长线与
的延长线与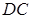 的延长线交于点
的延长线交于点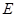 ,且
,且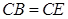 .
.
(Ⅰ)证明: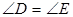 ;
;
(Ⅱ)设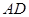 不是
不是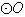 的直径,
的直径,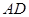 的中点为
的中点为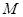 ,且
,且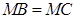 ,证明:
,证明: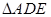 为等边三角形.
为等边三角形.
(本小题满分12分)已知函数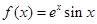
(1)求函数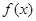 的单调区间;
的单调区间;
(2)当 时,
时,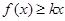 ,求实数
,求实数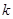 的取值范围
的取值范围
已知抛物线 的焦点为
的焦点为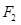 ,点
,点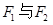 关于坐标原点对称,以
关于坐标原点对称,以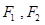 为焦点的椭圆
为焦点的椭圆 ,过点
,过点
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设 ,过点
,过点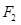 作直线
作直线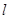 与椭圆
与椭圆 交于
交于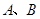 两点,且
两点,且 ,若
,若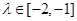 ,求
,求 的最小值。
的最小值。
(本小题满分12分)某校为了响应《中共中央国务院关于加强青少年体育增强青少年体质的意见》精神,落实“生命—和谐”教育理念和阳光体育行动的现代健康理念,学校特组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了 次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
| 甲 |
80 |
81 |
93 |
72 |
88 |
75 |
83 |
84 |
| 乙 |
82 |
93 |
70 |
84 |
77 |
87 |
78 |
85 |
(1)用茎叶图表示这两组数据
(2)从统计学的角度考虑,你认为选派那位学生参加比赛合适,请说明理由?
(3)若将频率视为概率,对甲同学在今后的三次比赛成绩进行预测,记这三次成绩高于 个/分钟的次数为
个/分钟的次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
(参考数据: ,
,
 )
)