近日,我市多个县区遭遇龙卷风,冰雹等自然灾害,某校八年级两个班各给灾区捐款1800元,已知(2)班比(1)班人均捐款多4元,(2)班的人数比(1)班的人数少10%,请你根据上述信息,就这两个班级的“人数”或“人均捐款”提出一个用分式方程解决的问题,并写出解题过程。
(本题8分)如图1,四边形OABC中,OA=a,OC=5,BC=3,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).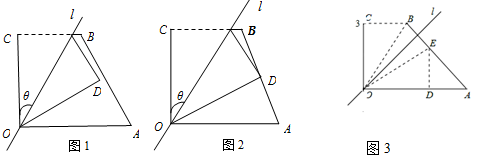
(1)若折叠后点D恰为AB的中点(如图2),求θ的值;
(2)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上,求a的值.
|
(本题8分)如图1,在四边形ABCD中,DC‖AB,AD=BC, BD平分∠ABC.
(1)求证:AD=DC;
(2)如图2,在上述条件下,若∠A=∠ABC= 60O,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.
(本题6分)如图,在正方形网格上的一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出 个三角形与△ABC全等.
(本题6分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.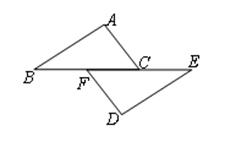
(1)选择的条件是(填序号)
(2)证明:
(本题8分)已知△ABC中,AB=AC,CD⊥AB于D.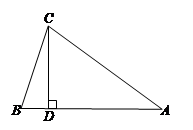
(1)若∠A=38º,求∠DCB的度数;
(2)若AB=5,CD=3,求BC的长.