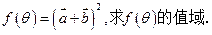(本小题满分10分)选修41:几何证明选讲
如图, 相交于A、B两点,AB是
相交于A、B两点,AB是 的直径,过A点作
的直径,过A点作 的切线交
的切线交 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与 、
、 交于C,D两点.
交于C,D两点.
求证:(1)PA·PD=PE·PC;
(2)AD=AE
(本小题满分14分) 已知圆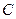 经过坐标原点, 且与直线
经过坐标原点, 且与直线 相切,切点为
相切,切点为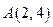 .
.
(1)求圆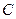 的方程;
的方程;
(2)若斜率为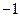 的直线
的直线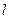 与圆
与圆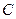 相交于不同的两点
相交于不同的两点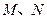 , 求
, 求 的取值范围..
的取值范围..
(本小题满分14分) 设数列 的前n项和为
的前n项和为 ,点
,点 均在函数y=3x-2的图像上。
均在函数y=3x-2的图像上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设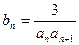 ,
, 是数列
是数列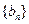 的前n项和,求使得
的前n项和,求使得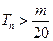 对所有
对所有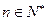 都成立的最大正整数
都成立的最大正整数 .
.
(本小题满分14分) 如图,在长方体
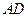
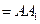
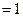

(1)证明:当点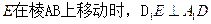 ;
;
(2)(理)在棱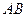 上是否存在点
上是否存在点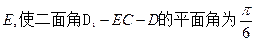 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 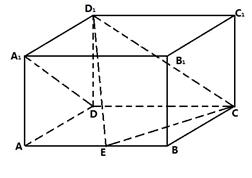
(文)在棱
 使
使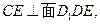 若存在,求出
若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
(本小题满分12分)某校从参加高二级期中考试的学生中抽出60名学生,将其成绩(均为整数)分成六段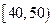 ,
,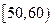 ,…,
,…,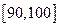 .后画出如下部分频率分布直方图.观察图形的信息,回答下列题:
.后画出如下部分频率分布直方图.观察图形的信息,回答下列题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分以上为及格);若统计方法中,同一组数据用该组区间的中点值作为代表,据此估计本次考试的平均分;
(3)从成绩是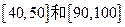 分的学生中选两人,求他们在同一分数段的概率.
分的学生中选两人,求他们在同一分数段的概率.
已知向量
(1)若 ∥
∥
(2)若