（1）如图1，△ABC中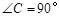，，请用直尺和圆规作一条直线，把△A-优题课

（1）如图1，△ABC中，，请用直尺和圆规作一条直线，把△ABC分割成两个等腰三角形，并在图上标出分割成的等腰三角形的底角的度数．（不写作法，但须保留作图痕迹）；
（2）已知内角度数的两个三角形如图2、图3所示．请你判断，能否分别画一条直线把它们分割成两个等腰三角形？若能，请在图上画出该直线并写出分割成的两个等腰三角形的底角的度数．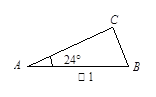

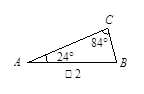
科目数学题型解答题难度中等

知识点：三角形的五心

先化简： $(\frac{x - 2}{x^{2} + 2 x} - \frac{x - 1}{x^{2} + 4 x + 4}) \div \frac{4 - x}{x}$ ，再选取一个适当的 $x$ 的值代入求值．

计算： ${(π - 3.14)}^{0} - {(\frac{1}{2})}^{- 2} + \sqrt[3]{27} - \sqrt{8}$ ．

如图，抛物线 $y = a x^{2} + bx + c$ 经过点 $A (- 2, 5)$ ，与 $x$ 轴相交于 $B (- 1, 0)$ ， $C (3, 0)$ 两点．

（1）求抛物线的函数表达式；

（2）点 $D$ 在抛物线的对称轴上，且位于 $x$ 轴的上方，将 $ΔBCD$ 沿直线 $BD$ 翻折得到△ $B C^{'} D$ ，若点 $C^{'}$ 恰好落在抛物线的对称轴上，求点 $C^{'}$ 和点 $D$ 的坐标；

（3）设 $P$ 是抛物线上位于对称轴右侧的一点，点 $Q$ 在抛物线的对称轴上，当 $ΔCPQ$ 为等边三角形时，求直线 $BP$ 的函数表达式．

如图1，在 $ΔABC$ 中， $AB = AC = 20$ ， $\tan B = \frac{3}{4}$ ，点 $D$ 为 $BC$ 边上的动点（点 $D$ 不与点 $B$ ， $C$ 重合）．以 $D$ 为顶点作 $∠ ADE = ∠ B$ ，射线 $DE$ 交 $AC$ 边于点 $E$ ，过点 $A$ 作 $AF ⊥ AD$ 交射线 $DE$ 于点 $F$ ，连接 $CF$ ．

（1）求证： $ΔABD ∽ ΔDCE$ ；

（2）当 $DE / / AB$ 时（如图 $2)$ ，求 $AE$ 的长；

（3）点 $D$ 在 $BC$ 边上运动的过程中，是否存在某个位置，使得 $DF = CF$ ？若存在，求出此时 $BD$ 的长；若不存在，请说明理由．

随着 $5 G$ 技术的发展，人们对各类 $5 G$ 产品的使用充满期待，某公司计划在某地区销售一款 $5 G$ 产品，根据市场分析，该产品的销售价格将随销售周期的变化而变化．设该产品在第 $x (x$ 为正整数）个销售周期每台的销售价格为 $y$ 元， $y$ 与 $x$ 之间满足如图所示的一次函数关系．

（1）求 $y$ 与 $x$ 之间的关系式；

（2）设该产品在第 $x$ 个销售周期的销售数量为 $p$ （万台）， $p$ 与 $x$ 的关系可以用 $p = \frac{1}{2} x + \frac{1}{2}$ 来描述．根据以上信息，试问：哪个销售周期的销售收入最大？此时该产品每台的销售价格是多少元？

试卷网试题网古诗词网作文网范文网