学校为了对某课题进行研究,用分层抽样方法从三个年级高一、高二、高三的相关老师中,抽取若干人组成研究小组,有关数据见下表(单位:人).
| 年级 |
相关人数 |
抽取人数 |
| 高一 |
18 |
x |
| 高二 |
36 |
2 |
| 高三 |
54 |
y |
(1)求x,y;
(2)若从高二、高三抽取的人中选2人做专题发言,求这2人都来自高三的概率。
已知函数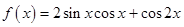 (
(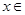 R).
R).
(1)求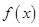 的最小正周期和最大值;
的最小正周期和最大值;
(2)若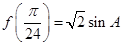 ,其中
,其中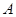 是面积为
是面积为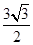 的锐角
的锐角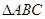 的内角,且
的内角,且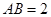 ,求边
,求边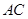 和
和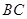 的长.
的长.
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重量(单位:克)是否合格,分别记录了6个抽查数据,获得重量数据的茎叶图如图4.
(1)根据样品数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对较稳定;
(2)若从乙车间6件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过2克的概率.
在等比数列 中,已知
中,已知
(1)求数列 的通项公式;
的通项公式;
(2)若 分别为等差数列
分别为等差数列 的第1项和第3项,设
的第1项和第3项,设 ,求数列
,求数列 的前项和
的前项和
在平面直角坐标系xOy中,已知曲线 ,将曲线
,将曲线 上所有点的横坐标伸长为原来的
上所有点的横坐标伸长为原来的 倍、纵坐标伸长为原来的2倍后得到曲线
倍、纵坐标伸长为原来的2倍后得到曲线 .以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
(Ⅰ)试写出直线 和曲线
和曲线 的直角坐标方程.
的直角坐标方程.
(Ⅱ)在曲线 上求一点
上求一点 ,使点
,使点 到直线
到直线 的距离最大,并求出此最大距离.
的距离最大,并求出此最大距离.
在极坐标系中,以点 为圆心,半径为3的圆
为圆心,半径为3的圆 与直线
与直线 交于
交于 两点.(1)求圆
两点.(1)求圆 及直线
及直线 的普通方程.
的普通方程.
(2)求弦长 .
.