在平面直角坐标系xOy中，已知曲线
，将曲线
上所有点的横坐标伸长为原来的
倍、纵坐标伸长为原来的2倍后得到曲线
.以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线
（Ⅰ）试写出直线
和曲线的直角坐标方程.
（Ⅱ）在曲线上求一点
，使点到直线的距离最大，并求出此最大距离.
已知函数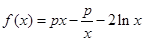
.
（1）若p=2，求曲线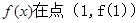
处的切线方程；
（2）若函数在其定义域内是增函数，求正实数p的取值范围；
（3）设函数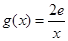
，若在[1,e]上至少存在一点
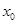，使得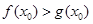
成立，求实数p的取值范围.
设正数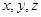
,
(1)满足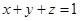
，求证：
；
(2)若
，求
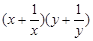的最小值。
从装有大小相同的2个红球和6个白球的袋子中，每摸出2个球为一次试验，直到摸出的球中有红球（不放回），则试验结束.
（Ⅰ）求第一次试验恰摸到一个红球和一个白球概率；
（Ⅱ）记试验次数为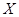
，求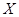的分布列及数学期望
．
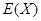已知函数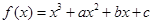
在
与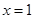
时都取得极值
(1)求
的值与函数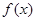
的单调区间
(2)若对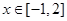
，不等式
恒成立，求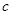
的取值范围。
已知数列{an}的前n项和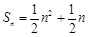
，
（1）求通项公式an ；（2）令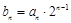
，求数列{bn}前n项的和Tn.