（本小题满分14分）
已知函数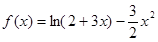
.
(1)求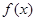
在[0,1]上的极值；
(2)若对任意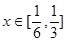
,不等式
成立,求实数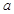
的取值范围；
(3)若关于
的方程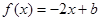
在[0,1]上恰有两个不同的实根,求实数
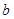的取值范围.
设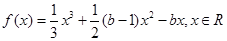
（1）当
时,求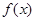
的单调区间；
（2）当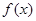
在R上有且仅有一个零点时,求
的取值范围.
如图，在三棱锥
中，
平面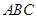
,
.
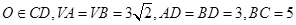（1）求证：
;
（2）当二面角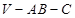
的平面角为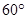
时，求三棱锥的体积.
已知函数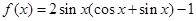
（1）求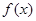
的最小正周期和最大值；
（2）若
为三角形的内角且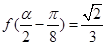
，求
的值
一个箱子里装有5个大小相同的球，有3个白球，2个红球，从中摸出2个球.
（1）求摸出的两个球中有1个白球和1个红球的概率；
（2）用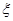
表示摸出的两个球中的白球个数，求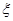的分布列及数学期望.
若
的图像关于直线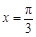
对称，其中
.
（Ⅰ）求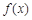
的解析式；
（Ⅱ）已知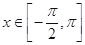
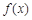，求的增区间；
（Ⅲ）将
的图像向左平移
个单位，再将得到的图像的横坐标变为原来的2倍（纵坐标不变）后得到的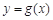
的图像；若函数
的图像与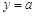
的图像有三个交点，求
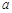的取值范围.