某班主任对全班50名学生进行了作业量多少的调查，喜欢玩电脑游戏的同学认为作业多的有18人，认为作业不多的有9人，不喜欢玩电脑游戏的同学认为作业多的有8人，认为作业不多的有15人.
（1）根据以上数据建立一个
的列联表；
（2）认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少？(参考数值：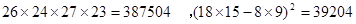
)
（本小题共14分）
已知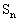
为数列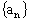
的前n项和，且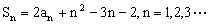
（I）求证：数列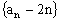
为等比数列；
（II）设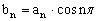
，求数列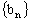
的前n项和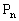
；
（III）设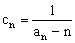
，数列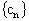
的前n项和为
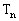，求证：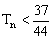
。
（本小题共14分）
已知函数
。
（I）当a=2时，求函数f(x)的单调区间；
（II）若不等式
对任意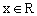
恒成立，求a的取值范围。
如图，直三棱柱
的侧棱长和底面边长都是
，截面
和截面
相交于
，求四面体
的体积．
 |
如图，已知一艘船从30 n mile/h的速度往北偏东
的Ａ岛行驶，计划到达Ａ岛后停留10 min后继续驶往Ｂ岛，Ｂ岛在Ａ岛的北偏西
的方向上．船到达Ｃ处时是上午10时整，此时测得Ｂ岛在北偏西
的方向，经过20 min到达Ｄ处，测得Ｂ岛在北偏西
的方向，如果一切正常的话，此船何时能到达Ｂ岛？
 |
经过两点
，
，且在
轴上截得的弦长为
的圆的方程．