每位同学都能感受到日出时美丽的景色．下图是一位同学从照片上剪切下来的画面，“图上”太阳与海平线交于A﹑B两点，他测得“图上”圆的半径为5厘米，AB=8厘米，若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟，求“图上”太阳升起的速度．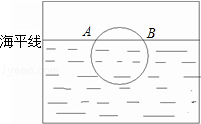
如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的直线互相垂直，垂足为D，且AC平分∠DAB．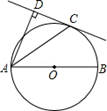
（1）求证：DC为⊙O的切线；
（2）若⊙O的半径为3，AD=4，求AC的长．
东台市为打造“绿色城市”，积极投入资金进行河道治污与园林绿化两项工程，已知2013年投资1000万元，预计2015年投资1210万元．若这两年内平均每年投资增长的百分率相同．
（1）求平均每年投资增长的百分率；
（2）按此增长率，计算2016年投资额能否达到1360万？
已知
是方程
的一个根，求
的值及方程的另一个根．
（1）x(x+4)=-5(x+4)；（2）
