如图,有多个长方形和正方形的卡片,图甲是选取了2块不同的卡片,拼成的一个图形,借助图中阴影部分面积的不同表示可以用来验证等式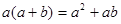 成立.
成立.
(1)根据图乙,利用面积的不同表示方法,写出一个代数恒等式 ;
(2)试写出一个与(1)中代数恒等式类似的等式,并用上述拼图的方法说明它的正确性.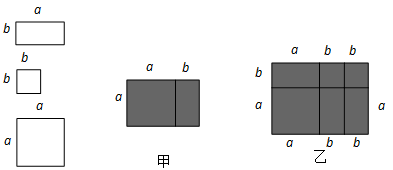
如图,在平面直角坐标系中,△ABC的三个顶点
坐标分别是A(2,3)、B(2,1)、C(3,2).
①判断△ABC的形状;②如果将△ABC沿着边AC旋转,求所得旋转体的全面积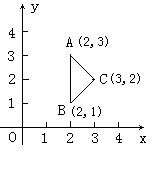
如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的格点上.
①在图甲中作出的四边形是中心对称图形但不是轴对称图形;
②在图乙中作出的四边形是轴对称图形但不是中心对称图形;
③在图丙中作出的四边形既是轴对称图形又是中心对称图形.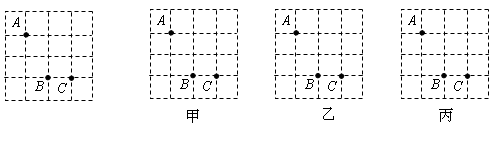
如图,已知:抛物线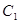 ,
,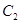 关于
关于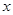 轴对称;抛物线
轴对称;抛物线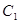 ,
,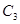 关于
关于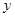 轴对称。
轴对称。
如果抛物线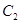 的解析式是
的解析式是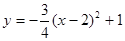 ,那么抛物线
,那么抛物线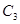 的解析式
的解析式
是.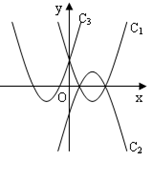
如图,在直角坐标系中,点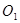 在
在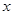 轴上,⊙
轴上,⊙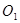 与
与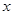 轴交于点
轴交于点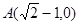 ,
,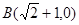 .直线
.直线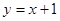 与坐标轴交于C 、D两点,直线在⊙
与坐标轴交于C 、D两点,直线在⊙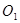 的左侧.
的左侧.求
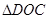 的面积;
的面积;当直线向右平移,第一次与⊙
 相切时,求直线的解析式.
相切时,求直线的解析式.
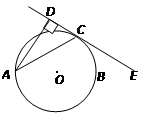
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.求证:直线CD为⊙O的切线;
当AB=2BE,且CE=时,求AD的长.
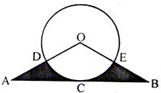
如图,△OAB的底边与⊙O相切,切点为C,且OA=OB,⊙O与OA、OB分别交于D、E两点,D、E分别为OA、OB的中点。求
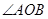 的度数;
的度数;若阴影部分的面积为
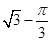 ,求⊙O的半径r
,求⊙O的半径r