借助“世博会”的东风,某小商品公司开发一种纪念品,每件产品的成本是15元,销售价是20元,月平均销售 件,通过改进工艺,产品的成本不变,质量得到提高,市场分析的结果表明:如果产品的销售价提高的百分率为
件,通过改进工艺,产品的成本不变,质量得到提高,市场分析的结果表明:如果产品的销售价提高的百分率为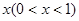 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为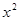 ,记改进工艺后,该公司销售纪念品的月平均利润是
,记改进工艺后,该公司销售纪念品的月平均利润是 元.
元.
(1)写出 与
与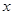 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该纪念品的销售价,使得公司销售该纪念品的月平均利润最大.
如图1,在直角梯形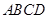 中,
中,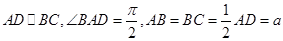 ,
,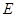 是
是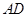 的中点,
的中点, 是AC与
是AC与 的交点,将
的交点,将 沿
沿 折起到图2中
折起到图2中 的位置,得到四棱锥
的位置,得到四棱锥 .
.

(Ⅰ)证明: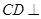 平面
平面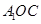 ;
;
(Ⅱ)当平面 平面
平面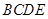 时,四棱锥
时,四棱锥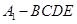 的体积为
的体积为 ,求
,求 的值.
的值.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.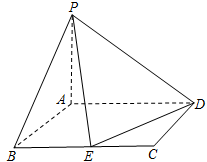
(1)证明:PE⊥DE;
(2)如果PA=2,求异面直线AE与PD所成的角的大小.
如图,在四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(1)证明:EF∥平面PAD;
(2)求三棱锥EABC的体积V.
四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.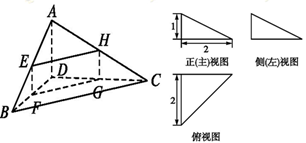
(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
已知函数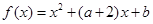 ,
,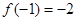 ,对于
,对于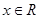 ,
,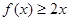 恒成立.
恒成立.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设函数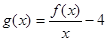 .
.
①证明:函数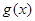 在区间在
在区间在 上是增函数;
上是增函数;
②是否存在正实数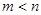 ,当
,当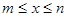 时函数
时函数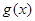 的值域为
的值域为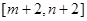 .若存在,求出
.若存在,求出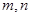 的值,若不存在,则说明理由.
的值,若不存在,则说明理由.