已知 ,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
(Ⅰ)求n的值;
(Ⅱ)求a1+a2+a3+……+an的值。
2008年底某县的绿化面积占全县总面积的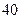 %,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
%,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
⑴设该县的总面积为1,2008年底绿化面积为 ,经过
,经过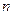 年后绿化的面积为
年后绿化的面积为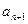 ,试用
,试用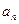 表示
表示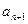 ;
;
⑵求数列 的第
的第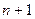 项
项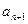 ;
;
⑶至少需要多少年的努力,才能使绿化率超过60%(参考数据: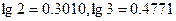 )
)
在一直线上共插有13面小旗,相邻两面之距离为 ,在第一面小旗处有某人把小旗全部集中到一面小旗的位置上,每次只能拿一面小旗,要使他走的路最短,应集中到哪一面小旗的位置上?最短路程是多少?
,在第一面小旗处有某人把小旗全部集中到一面小旗的位置上,每次只能拿一面小旗,要使他走的路最短,应集中到哪一面小旗的位置上?最短路程是多少?
已知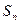 为数列
为数列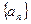 的前
的前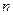 项和,点
项和,点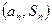 在直线
在直线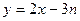 上.
上.
⑴若数列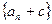 成等比,求常数的值;
成等比,求常数的值;
⑵求数列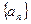 的通项公式;
的通项公式;
⑶数列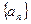 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;
若不存在,请说明理由.
用砖砌墙,第一层(底层)用去了全部砖块的一半多一块,第二层用去了剩下的一半多一块,…依次类推,每一层都用去了上次剩下的砖块的一半多一块,到第十层恰好把砖块用完,问共用了多少块?
设函数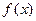 的定义域为
的定义域为 ,当
,当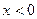 时,
时, ,且对任意的实数
,且对任意的实数 ,有
,有 .
.
⑴求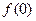 ,判断并证明函数
,判断并证明函数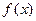 的单调性;
的单调性;
⑵数列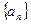 满足
满足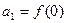 ,且
,且
①求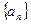 通项公式;
通项公式;
②当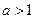 时,不等式
时,不等式 对不小于
对不小于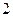 的正整数恒成立,求
的正整数恒成立,求 的取值范围.
的取值范围.